Diferență între revizuiri ale paginii „CID Seminar 6”
| (Nu s-au afișat 4 versiuni intermediare efectuate de același utilizator) | |||
| Linia 40: | Linia 40: | ||
'''Soluție:''' | '''Soluție:''' | ||
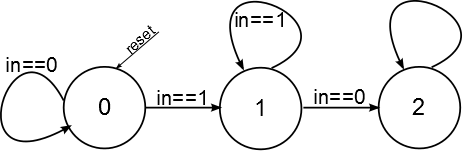
| − | + | 1. Automatul va avea 3 stări: starea inițială, în care așteaptă 0, starea în care așteaptă 1 și starea de eroare, când o valoare de 0 a fost detectată după secvența de 1. Astfel, diagrama de stări este următoarea: | |
| − | + | [[Fișier:sem6_fig2.png]] | |
| − | + | 2. Cum numărul de stări este 3, vom avea nevoie de 2 biți pentru registrul de stare. | |
| + | |||
| + | 3. | ||
<syntaxhighlight lang="verilog"> | <syntaxhighlight lang="verilog"> | ||
module FSM( | module FSM( | ||
| Linia 125: | Linia 127: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | Aceste notațiile le putem folosi apoi în locul valorilor | + | Aceste notațiile le putem folosi apoi în locul valorilor: |
| + | |||
| + | <syntaxhighlight lang="verilog"> | ||
| + | always @(posedge clock) begin | ||
| + | if (reset) begin | ||
| + | state <= STATE_READ_0; | ||
| + | end else begin | ||
| + | case (state) | ||
| + | STATE_READ_0: if (in == 1) state <= STATE_READ_1; | ||
| + | STATE_READ_1: if (in == 0) state <= STATE_ERROR; | ||
| + | STATE_ERROR : ; // do nothing | ||
| + | default : state <= STATE_READ_0; | ||
| + | endcase | ||
| + | end | ||
| + | end | ||
| + | |||
| + | assign detectOk = (state == STATE_READ_0) || (state == STATE_READ_1); | ||
| + | assign detectFail = (state == STATE_ERROR); | ||
| + | </syntaxhighlight> | ||
== Exemplul 2 == | == Exemplul 2 == | ||
Versiunea curentă din 28 aprilie 2014 11:57
În acest seminar vi se va prezenta noțiunea de automat finit și modul de descriere al acestuia în Verilog.
Cuvinte cheie: automat finit, FSM (Finite State Machine), Mealy, Moore, stare, tranziție Sintaxa Verilog: localparam
Automatul finit, numit și FSM (Finite State Machine), este un model matematic de computație, definit de următoarele elemente:
- O mulțime finită de simboluri de intrare, numită alfabet de intrare;
- O mulțime finită și nevidă de simboluri de ieșire, numită alfabet de ieșire;
- O mulțime finită și nevidă de stări, din care doar una, numită starea curentă, este activă la un moment dat;
- O stare inițială, care face parte din mulțimea stărilor;
- O funcție de tranziție a stărilor, care calculează starea următoare a automatului în funcție de starea curentă și de simbolul de intrare;
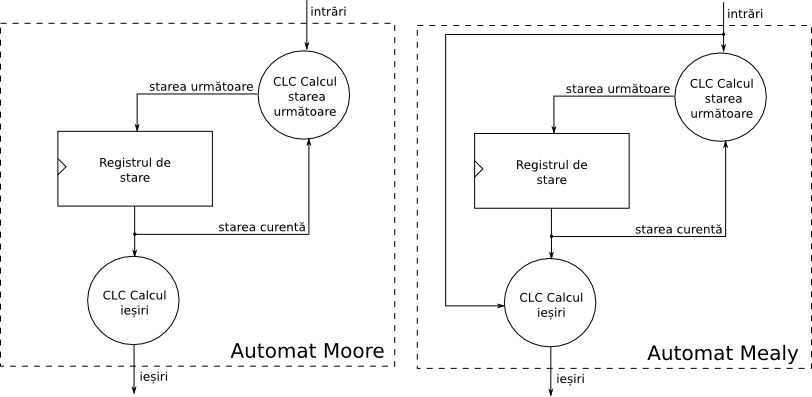
- O funcție de calcul a ieșirii, care determină simbolul de ieșire în funcție de starea curentă (în cazul automatelor de tip Moore) sau în funcție de starea curentă și de simbolul de intrare (în cazul automatelor de tip Mealy).
În sistemele digitale, un automat finit este utilizat pentru a programa o secvență de operații și se poate implementa ca un circuit secvențial. Astfel, simbolurile de intrare și de ieșire vor fi reprezentate de toate combinațiile posibile de intrare, respectiv de ieșire, ale circuitului. Funcția de tranziție a stărilor și funcția de calcul a ieșirii vor fi implementate ca circuite logice combinaționale (CLC-uri), iar starea curentă a automatului va fi memorată într-un registru intern.
La fiecare front al ceasului, valoarea stării următoare, calculată de către CLC, va fi încărcată în registru. Dacă registrul are n biți, numărul maxim de stări care pot fi reprezentate este 2n. Acest număr poate fi mai mic, în funcție de schema de codare a stărilor. De exemplu, pentru n = 4, folosind codarea binară se pot reprezenta cel mult 16 stări (0000, 0001, 0010, ..., 1111), în timp ce pentru codarea one-hot, în care doar un singur bit poate lua valoarea 1, se pot reprezenta 4 stări (1000, 0100, 0010, 0001).
Întrebare: Care este cel mai simplu automat cu care v-ați întâlnit până acum?
Stările și tranzițiile dintre acestea se pot reprezenta în diferite moduri. Cel mai folosit dintre acestea este diagrama de stări, în care stările și tranzițiile sunt reprezentate sub forma unui graf orientat. Alt mod posibil de reprezentare este tabelul de tranziție al stărilor, similar unui tabel de adevăr.
Exemplul 1
Definiți stările și tranzițiile necesare pentru un automat finit care să recunoască secvența de intrare 0n1m, cu n, m ≥ 0. Desenați diagrama de stări. Descrieți comportamental circuitul în Verilog. Realizați un modul de test pentru acest circuit.
Ce tip de automat ați implementat?
Explicații suplimentare:
Pașii pentru descrierea comportamentală a unui automat finit sunt următorii:
- Analizați cerința și desenați diagrama de stări;
- Numărați stările și stabiliți numărul de biți de care aveți nevoie pentru registrul de stare;
- Definiți modulul în Verilog, adăugând intrările, ieșirile și registrul de stare intern;
- Folosind un bloc always secvențial și un bloc condițional case, descrieți toate tranzițiile posibile către alte stări, pentru fiecare stare posibilă;
- Definiți și descrieți ieșirile combinaționale în funcție de starea curentă și de intrări.
Soluție:
1. Automatul va avea 3 stări: starea inițială, în care așteaptă 0, starea în care așteaptă 1 și starea de eroare, când o valoare de 0 a fost detectată după secvența de 1. Astfel, diagrama de stări este următoarea:
2. Cum numărul de stări este 3, vom avea nevoie de 2 biți pentru registrul de stare.
3.
module FSM(
input clock,
input reset,
input in,
output detectOk,
output detectFail
);
reg [1:0] state;
always @(posedge clock) begin
if (reset) begin
state <= 2'b00;
end else begin
case (state)
2'b00: if (in == 1) state <= 2'b01;
2'b01: if (in == 0) state <= 2'b10;
2'b10: ; // do nothing
default: state <= 2'b00;
endcase
end
end
assign detectOk = (state == 2'b00) || (state == 2'b01);
assign detectFail = (state == 2'b10);
endmodule
module FsmTest;
reg clock;
reg reset;
reg in;
wire detectOk;
wire detectFail;
initial begin
clock = 0;
forever #1 clock = ~clock;
end
initial begin
in = 0;
reset = 0;
#2 reset = 1;
#2 reset = 0;
#6 in = 1;
#10 in = 0;
#10 $stop();
end
FSM dut(
.clock(clock),
.reset(reset),
.in(in),
.detectOk(detectOk),
.detectFail(detectFail)
);
endmodule
Observați că, odată ajuns într-una din stările finale, automatul se blochează. Pentru a putea trece înapoi în starea inițială, este necesar un semnal de reset. Prin urmare:
Observați că avem o stare nefolosită. În general, ca regulă de bună practică, pentru toate stările nefolosite, care sunt reprezentate de cazul default din blocul case, tranziția următoare va fi întotdeauna către starea inițială (de reset).
Observați că stările sunt definite ca valori. Pentru un număr mare de stări, codurile vor deveni greu de înțeles. Prin urmare, introducem următoarele notații în modul:
localparam STATE_READ_0 = 2'b00;
localparam STATE_READ_1 = 2'b01;
localparam STATE_ERROR = 2'b10;
Aceste notațiile le putem folosi apoi în locul valorilor:
always @(posedge clock) begin
if (reset) begin
state <= STATE_READ_0;
end else begin
case (state)
STATE_READ_0: if (in == 1) state <= STATE_READ_1;
STATE_READ_1: if (in == 0) state <= STATE_ERROR;
STATE_ERROR : ; // do nothing
default : state <= STATE_READ_0;
endcase
end
end
assign detectOk = (state == STATE_READ_0) || (state == STATE_READ_1);
assign detectFail = (state == STATE_ERROR);
Exemplul 2
Descrieți structural modulul de la exemplul anterior, astfel:
- Cele două CLC-uri vor fi definite ca module separate;
- Automatul va fi un modul „de top”, în care instanțiați cele două CLC-uri și registrul de stare.
Testați automatul cu modulul de test de la exercițiul anterior.
Exemplul 3
Realizați un automat finit pentru o mașină care vinde ciocolată CMOS, care costă 2,5 lei. Automatul acceptă monede de 50 de bani și bancnote de 1 leu. Denumiți starea curentă în funcție de suma acumulată în prezent, exprimată în multipli întregi de 50 de bani (de exemplu STATE_0_BANI, STATE_50_BANI, STATE_100_BANI etc.). Când se ajunge la suma de 2,5 lei sau mai mult, automatul va livra o ciocolată și va relua procesul, scăzând 2,5 lei din suma curentă. Automatul nu restituie restul.
Ce tip de automat ați implementat?
Explicații suplimentare:
Circuitul trebuie să aibă următoarele porturi:
- input load50bani – activ când este introdusă o monedă de 50 de bani
- input load1leu – activ când este introdusă o bancnotă de 1 leu
- output ack50bani – activ când automatul detectează inserția unei monede de 50 de bani
- output ack1leu – activ când automatul detectează inserția unei bancnote de 1 leu
- output productDelivered – activ când este livrată o ciocolată
De ce este nevoie de porturile „ack”?
Exemplul 4
Dacă una sau mai multe din intrările automatului sunt asincrone (își schimbă valoarea independent de frontul de ceas), atunci și intrarea registrului de stare iși poate schimba valoarea asincron. Astfel, pentru a se evita tranziția într-o stare nedefinită, sau într-o stare în care automatul nu trebuie să ajungă din starea curentă, toate stările sunt codate astfel încât între codul stării curente și codul stării următoare să difere doar un singur bit. Acest mod de codare se numește cod Gray.
În primul nostru exemplu, aveam 3 stări:
- STATE_READ_0, codată 2'b00
- STATE_READ_1, codată 2'b01
- STATE_ERROR, codată 2'b10
Se observă aici că starea STATE_ERROR e adiacentă stării STATE_READ_1, dar codările lor diferă prin ambii biți, prin urmare acesta nu este un cod Gray. Dacă, să spunem, ne aflăm în starea STATE_READ_1 (2’b01) și intrarea automatului este 1, atunci CLC-ul care calculează starea următoare va avea la ieșire tot 2’b01. Dar, în momentul în care intrarea automatului se schimbă în 0, atunci această modificare propagă prin porți la ieșirea CLC-ului, schimbându-i valoarea acesteia în 2’b10 (starea de eroare). Totuși, știm că aceste două semnale nu pot ajunge EXACT în același timp, deci e posibil ca bitul mai puțin semnificativ să se schimbe primul, caz în care, pentru un foarte scurt interval de timp, ieșirea CLC-ului va fi 2’b00 până când ajunge la valoarea corectă de 2’b10. Similar, cel mai semnificativ bit se poate schimba primul, ducând valoarea în 2’b11 până când se stabilizează din nou în 2’b10. În ambele aceste situații, dacă valoarea greșită este memorată în registrul de stare, acest lucru implică o tranziție eronată, ori din starea STATE_READ_1 în STATE_READ_0, ori în starea invalidă 2’b11.
Putem reface codurile stărilor astfel:
- STATE_READ_0, codată 2'b00
- STATE_READ_1, codată 2'b01
- STATE_ERROR, codată 2'b11
Analizați tranzițiile posibile datorate intrării asincrone. Ce observați?
Realizați un numărător Gray pe 4 biți astfel încât oricare două valori consecutive să difere prin fix un bit. Scrieți un modul de test pentru acest circuit prin care să verificați că se comportă corect.
Temă
Modificați automatul de la exemplul 3, astfel încât să dea rest.