Diferență între revizuiri ale paginii „Introducere. SystemVerilog HDL”
| Linia 27: | Linia 27: | ||
==== Sistemul de numerație binar ==== | ==== Sistemul de numerație binar ==== | ||
| − | Sistemul binar este un sistem de numerație bazat pe [http://en.wikipedia.org/wiki/Boolean_algebra_(logic) algebra booleană]. Acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 10<sup>4</sup>, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza | + | Sistemul binar este un sistem de numerație bazat pe [http://en.wikipedia.org/wiki/Boolean_algebra_(logic) algebra booleană]. Acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 10<sup>4</sup>, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza 2, un 1 pe pozitia 4 este echivalent cu valoarea 1 * 2<sup>4</sup>. Aceasta este și regula de transformare a numerelor din baza 2 în baza 10. Prin urmare: |
| + | |||
| + | 1001010<sub>(2)</sub> = 0 * 2<sup>0</sup> + 1 * 2<sup>1</sup> + 0 * 2<sup>2</sup> + 1 * 2<sup>3</sup> + 0 * 2<sup>4</sup> + 0 * 2<sup>5</sup> + 1 * 2<sup>6</sup> = 0 + 2 + 0 + 8 + 0 + 0 + 64 = 54<sub>(10)</sub> | ||
== Implementarea circuitelor digitale folosind FPGA == | == Implementarea circuitelor digitale folosind FPGA == | ||
Versiunea de la data 17 ianuarie 2012 14:59
Introducere în Circuite Digitale
Semnale analogice
Începând cu lecțiile de electrocinetică de la orele de fizică din liceu (surse de tensiune, rezistențe, condensatoare, bobine, etc.) și terminând cu orele de Dispozitive și Circuite Electronice, sistemele studiate au fost formate din componente formând ciruite analogice. Circuitele analogice sunt circuite în care mărimile studiate (curent, tensiune), variază continuu în anumite intervale. Un exemplu concret este un amplificator audio, care preia un semnal sonor analogic și îl amplifică pentru a putea fi transmis mai departe, la un sistem de boxe. Puteți vedea un exemplu de semnal analogic în figura alăturată. Desigur, această imagine este generată de un computer, care este un dispozitiv digital, astfel ea nu poate reprezenta un semnal analogic adevărat ci poate doar simula un astfel de semnal, cu o anumită precizie.
Semnale digitale
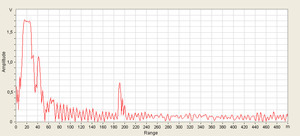
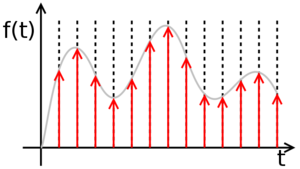
Un semnal digital este o înșiruire de valori discrete, fiecare din aceste valori făcând parte dintr-o mulțime discretă de valori raționale. Transformarea unui semnal analogic într-un semnal digital, implică o pierdere de precizie. Să luăm spre exemplu un semnal analogic sinusiodal simplu, reprezentând variația în timp a tensiunii la bornele unui rezistor. Între momentele t=0 și t=1, funcția, fiind continuă, are o infinitate de valori, prin urmare este imposibil de a izola fiecare valoare în parte, șirul astfel obținut fiind infinit. Procedura, în această situație, este de a izola doar o parte din valori, la anumite momente de timp, numite eșantioane, astfel încât să obținem un șir finit de valori. Această procedură se numește eșantionare, iar perioada de timp dintre două eșantioane succesive, poartă numele de perioadă de eșantionare. Cu cât perioada de eșantionare este mai mică (respectiv frecvența de eșantionare mai mare), cu atât semnalul digital obținut este o copie mai fidelă (pierdere mai mica de precizie) față de semnalul analogic original. Dacă totuși semnalul analogic este de bandă limitată (adică poate fi scris ca o sumă finită de semnale sinusoidale), atunci teorema eșantionării arată că dacă eșantionarea se face cu o frecvență de cel puțin de două ori mai mare decât frecvența maximă din spectrul semnalului, din seria de eșantioane se poate obține cu precizie de 100% semnalul analogic original.
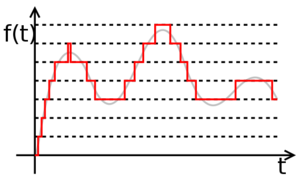
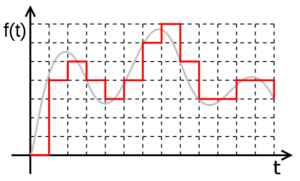
Totuși, mai există o problemă. Semnalul fiind continuu, valorile eșantioanele se află într-un spațiu continuu, prin urmare de precizie infinită. Pentru a reduce precizia valorilor, se utilizează un procedeu numit cuantizare. Acest procedeu implică împărțirea intervalului de valori posibile pentru semnal în subdiviziuni. Cu cât aceste subdiviziuni sunt mai fine, cu atât valorile obținute prin cuantizare vor fi mai aproape de valorile reale ale semnalului original, dar vor fi reprezentate cu un număr mai pare de simboluri.
În concluzie, un semnal digital este o înșiruire de numere, obținute prin eșantionarea și cuantizarea unui semnal analogic.
Numere și simboluri. Baze de numerație
După cum s-a observat în capitolul anterior, un semnal digital este o înșiruire de valori. Aceste valori sunt reprezentate folosind simboluri, aparținând unei baze de numerație. Cel mai simplu exemplu este cel cu care suntem obișnuiți cu toții, adică baza zecimală, folosind ca simboluri cifrele de la 0 la 9. Dar acesta nu este nici pe departe singurul. Alte exemple ar fi sistemul de numerație roman, unde se folosesc ca simboluri literele I, V, X, L, C, D și M, unde valoarea acestor simboluri intr-un număr depinde de ordinea lor. Același lucru îl putem spune și despre baza de numerație zecimala, unde, spre exemplu, simbolul 9 are altă valoare dacă se află pe prima poziție (9) decât dacă se află pe a doua (90). Ce este interesant de reținut este că, în ciuda asocierii mentale dintre simbolurile cu care am fost obișnuiți de mici să lucrăm și valorile numerice pe care acestea le exprimă, cele două noțiuni sunt complet distincte. Valoarea „zece” poate fi exprimată numeric în baza zecimala ca 10, în sistemul de numerație roman ca X, în sistemul hexazecimal ca A, în sistemul binar ca 1010, în cel octal ca 12, dar toate aceste reprezentări exprimă, de fapt, același număr.
Sistemul de numerație binar
Sistemul binar este un sistem de numerație bazat pe algebra booleană. Acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 104, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza 2, un 1 pe pozitia 4 este echivalent cu valoarea 1 * 24. Aceasta este și regula de transformare a numerelor din baza 2 în baza 10. Prin urmare:
1001010(2) = 0 * 20 + 1 * 21 + 0 * 22 + 1 * 23 + 0 * 24 + 0 * 25 + 1 * 26 = 0 + 2 + 0 + 8 + 0 + 0 + 64 = 54(10)
Implementarea circuitelor digitale folosind FPGA
În lumea înconjuratoare, omul se confruntă cu o mare diversitate de probleme. Aceste probleme au diverse moduri de rezolvare:
- Hardware
- Software
- mixte: Hardware-Software (specific pentru majoritatea sistemelor complexe)
module Counter(
input [7:0] in0,
input [7:0] in1,
output [8:0] out
);
assign out = in0 + in1;
endmodule