Diferență între revizuiri ale paginii „Introducere. SystemVerilog HDL”
| (Nu s-au afișat 39 de versiuni intermediare efectuate de alți 4 utilizatori) | |||
| Linia 5: | Linia 5: | ||
=== Semnale analogice === | === Semnale analogice === | ||
| − | Începând cu lecțiile de electrocinetică de la orele de fizică din liceu (surse de tensiune, rezistențe, condensatoare, bobine, etc.) și terminând cu orele de [[Dispozitive și Circuite Electronice]], sistemele studiate au fost formate din componente formând | + | Începând cu lecțiile de electrocinetică de la orele de fizică din liceu (surse de tensiune, rezistențe, condensatoare, bobine, etc.) și terminând cu orele de [[Dispozitive și Circuite Electronice]], sistemele studiate au fost formate din componente formând circuite analogice. Circuitele analogice sunt circuite în care mărimile studiate (curent, tensiune), variază continuu în anumite intervale. Un exemplu concret este un amplificator audio, care preia un semnal sonor analogic și îl amplifică pentru a putea fi transmis mai departe, la un sistem de boxe. Puteți vedea un exemplu de semnal analogic în figura alăturată. Desigur, această imagine este generată de un computer, care este un dispozitiv digital, astfel ea nu poate reprezenta un semnal analogic adevărat ci poate doar simula un astfel de semnal, cu o anumită precizie. |
=== Semnale digitale === | === Semnale digitale === | ||
| Linia 27: | Linia 27: | ||
==== Sistemul de numerație binar ==== | ==== Sistemul de numerație binar ==== | ||
| − | + | După cum îi spune și numele, acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 10<sup>4</sup>, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza 2, un 1 pe pozitia 4 este echivalent cu valoarea 1 * 2<sup>4</sup>. Aceasta este și regula de transformare a numerelor din baza 2 în baza 10. Prin urmare: | |
| − | 1001010<sub>(2)</sub> = | + | 1001010<sub>(2)</sub> = 1 * 2<sup>6</sup> + 0 * 2<sup>5</sup> + 0 * 2<sup>4</sup> + 1 * 2<sup>3</sup> + 0 * 2<sup>2</sup> + 1 * 2<sup>1</sup> + 0 * 2<sup>0</sup> = 64 + 0 + 0 + 8 + 0 + 2 + 0 = 54<sub>(10)</sub> |
Transformarea unui număr din baza zecimală în cea binară implică împărțirea repetată la 2 (numărul de simboluri ale bazei), unde deîmpărțitul la fiecare iterație este dat de câtul împărțirii anterioare. Operația se repetă cât timp câtul este diferit de 0. Numărul în baza binară este dat de secvența resturilor începând cu ultima împărțire și terminând cu prima. | Transformarea unui număr din baza zecimală în cea binară implică împărțirea repetată la 2 (numărul de simboluri ale bazei), unde deîmpărțitul la fiecare iterație este dat de câtul împărțirii anterioare. Operația se repetă cât timp câtul este diferit de 0. Numărul în baza binară este dat de secvența resturilor începând cu ultima împărțire și terminând cu prima. | ||
| − | + | Avantajul sistemului binar este că numărul redus de simboluri face ca și numărul de operații posibile între două simboluri aleatoare să fie redus, prin urmare este ușor de imaginat o realizare fizică a unor circuite care să implementeze aceste operații. Dezavantajul este că pentru numere relativ mici, este nevoie de multe simboluri pentru reprezentare. Așadar, pentru flexibilitatea operației cu valori reprezentate cu multe simboluri, se utilizeaza baza de numerație hexazecimală, adică baza 16. După cum îi spune și numele, baza hexazecimală utilizează 16 simboluri: cifrele de la 0 la 9, și caracterele a, b, c, d, e și f. Utilizarea bazei 16 este avantajoasă datorită trecerii foarte ușoare între ea și baza 2. Astfel, la orice valoare reprezentată printr-o secvență de patru simboluri binare corespunde unul și numai un simbol hexazecimal. | |
| − | + | === Computație și control === | |
| − | === | + | Am ajuns deci la concluzia că se pot face calcule (computație) folosind doar două simboluri, corespunzătoare valorilor de zero și de unu. Avem la dispoziție o bază de numerație (baza doi), prin care se pot face calcule din cele mai complexe, cu aceeași acuratețe ca și cele din baza decimală. Dar pe lângă calculul efectiv, un sistem informatic trebuie să poată lua decizii, adică să poate evalua o expresie și să decidă valoarea acesteia de adevăr, operație de tipul general '''if then else'''. Cel mai simplu exemplu de funcție care nu se poate calcula fără luarea unei decizii, este funcția modul (de fapt, orice funcție cu ramuri). Aceasta este de forma: |
| + | <syntaxhighlight lang="Pascal"> | ||
| + | if (operand < 0) then (result = -operand) else (result = operand); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Expresia (operand < 0) este ceea ce se numește o expresie logică. Expresiile logice, în [http://en.wikipedia.org/wiki/Boolean_algebra algebra booleană], pot lua numai două valori: '''''adevărat''''' sau '''''fals'''''. Aceste valori pot fi notate cu aceleași simboluri pe care le utilizăm pentru valori numerice în baza doi, adică '''''0''''' pentru valoarea de adevăr '''''fals (false)''''' și '''''1''''' pentru valoarea de adevăr '''''adevărat (true)'''''. | ||
| + | |||
| + | Cum asupra valorilor numerice pot fi aplicați operatori numerici (adunare, scădere, înmulțire), și asupra valorilor logice, pot fi aplicați operatori logici (ȘI, SAU, NU, SAU EXCLUSIV). Aceștia sunt explicați în detaliu pe pagina Wikipedia a [http://en.wikipedia.org/wiki/Boolean_algebra algebrei booleane]. | ||
| + | |||
| + | Concluzia este că folosind aceleași două simboluri, putem face calcule, folosind algebra binară, dar putem exercita control asupra unei funcții, folosind algebra booleană. După cum simbolurile se suprapun pentru computație și control, și operatorii asociați pot avea aceeași formă, și atunci distincția se face doar prin interpretarea lor. Spre exemplu, tabelul cu rezultate pentru înmulțirea a două numere de un bit (operație numerică) arată în felul următor: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- bgcolor="#ddeeff" align="center" | ||
| + | |colspan=2|'''INTRARE''' || '''IEȘIRE''' | ||
| + | |- bgcolor="#ddeeff" align="center" | ||
| + | | A || B || A * B | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |0 || 0 || 0 | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |0 || 1 || 0 | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |1 || 0 || 0 | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |1 || 1 || 1 | ||
| + | |} | ||
| + | |||
| + | În același timp, operația logică ȘI care întoarce 1 dacă și numai dacă ambii operanzi sunt 1 (mă duc la film DACĂ nu plouă ȘI am bani), are următorul tabel de adevăr: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- bgcolor="#ddeeff" align="center" | ||
| + | |colspan=2|'''INTRARE''' || '''IEȘIRE''' | ||
| + | |- bgcolor="#ddeeff" align="center" | ||
| + | | A || B || A ȘI B | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |0 || 0 || 0 | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |0 || 1 || 0 | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |1 || 0 || 0 | ||
| + | |- bgcolor="#ddffdd" align="center" | ||
| + | |1 || 1 || 1 | ||
| + | |} | ||
| + | |||
| + | Se observă că cele două funcții sunt identice. În acest fel, distincția dintre valoare logică și valoare numerică (respectiv operator logic și operator numeric) ține de interpretarea valorilor de intrare (dacă acestea sunt valori logice sau numerice) iar implementarea operatorilor este identică (prin urmare circuitul asociat este identic). | ||
| + | |||
| + | === Circuite === | ||
[[Fișier:Not_gate.png|thumb|Simbol inversor(A - intrare, out - ieșire)]] | [[Fișier:Not_gate.png|thumb|Simbol inversor(A - intrare, out - ieșire)]] | ||
[[Fișier:CMOS_inverter.png|thumb|Inversor alcătuit din tranzistoare CMOS]] | [[Fișier:CMOS_inverter.png|thumb|Inversor alcătuit din tranzistoare CMOS]] | ||
| − | În electronica digitală, ca de fapt în toată ramura tehnologiei care lucrează cu circuite digitale (adică calculatoare) ca și în teroria informației, un element care poate lua o valoare binară asociată unui simbol binar, se numește [http://en.wikipedia.org/wiki/Bit bit]. Baza circuitelor digitale, oricât de complexe, este dată de sub-circuitele care calculează operațiile unare și binare (adică care care au unul respectiv doi operanzi) între doi biți. Un astfel de sub-circuit se numește poartă (en:[http://en.wikipedia.org/wiki/Logic_gate gate]). | + | În electronica digitală, ca de fapt în toată ramura tehnologiei care lucrează cu circuite digitale (adică calculatoare) ca și în teroria informației, un element care poate lua o valoare binară asociată unui simbol binar, se numește [http://en.wikipedia.org/wiki/Bit bit]. Baza circuitelor digitale, oricât de complexe, este dată de sub-circuitele care calculează operațiile unare și binare (adică care care au unul respectiv doi operanzi) între doi biți. Un astfel de sub-circuit se numește poartă (en:[http://en.wikipedia.org/wiki/Logic_gate gate]). Aceeași poartă poate fi considerată implementarea unui operator numeric de un bit, dar și implementarea unui operator logic. |
| − | Modul de codare a valorilor asociate simbolurilor binare, în electronica digitală este printr-o diferență de potențial între două puncte. În tehnologia curentă utilizată ([http://en.wikipedia.org/wiki/CMOS CMOS]), o tensiune între 0 și Vdd/2 este asociată valorii binare de 0 iar o tensiune între Vdd/2 și Vdd valorii binare de 1.[http://en.wikipedia.org/wiki/Logic_level] | + | Modul de codare a valorilor asociate simbolurilor binare, în electronica digitală, este printr-o diferență de potențial între două puncte. În tehnologia curentă utilizată ([http://en.wikipedia.org/wiki/CMOS CMOS]), o tensiune între 0 și Vdd/2 este asociată valorii binare de 0 iar o tensiune între Vdd/2 și Vdd valorii binare de 1.[http://en.wikipedia.org/wiki/Logic_level] |
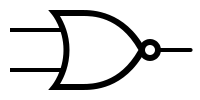
Cea mai simplă poartă este cea care implementează operația logică de negare (are o singură intrare și o singură ieșire care este intotdeauna diferită de cea de intrare, adică pentru intrarea 0, ieșirea este 1 și pentru intrarea 1, ieșirea este 0). Această poartă se numește inversor, sau poartă NU (en: [http://en.wikipedia.org/wiki/Inverter_(logic_gate) inverter], NOT gate). | Cea mai simplă poartă este cea care implementează operația logică de negare (are o singură intrare și o singură ieșire care este intotdeauna diferită de cea de intrare, adică pentru intrarea 0, ieșirea este 1 și pentru intrarea 1, ieșirea este 0). Această poartă se numește inversor, sau poartă NU (en: [http://en.wikipedia.org/wiki/Inverter_(logic_gate) inverter], NOT gate). | ||
| Linia 51: | Linia 96: | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | ! Tip !! Simbol !! | + | ! Tip !! Simbol !! Tabel de adevăr !! Tip !! Simbol !! Tabel de adevăr |
|- | |- | ||
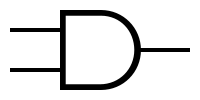
| '''AND''' | | '''AND''' | ||
| − | | [[Image: | + | | [[Image:and.png|AND symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 71: | Linia 115: | ||
|1 || 1 || 1 | |1 || 1 || 1 | ||
|} | |} | ||
| − | |||
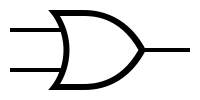
| '''OR''' | | '''OR''' | ||
| − | | [[Image: | + | | [[Image:or.png|OR symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 92: | Linia 134: | ||
|- | |- | ||
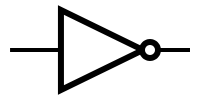
| '''NOT''' | | '''NOT''' | ||
| − | | [[Image: | + | | [[Image:not.png|NOT symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 105: | Linia 146: | ||
|1 || 0 | |1 || 0 | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
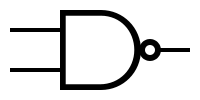
| '''NAND''' | | '''NAND''' | ||
| − | | [[Image: | + | | [[Image:nand.png|NAND symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 128: | Linia 165: | ||
|- | |- | ||
| '''NOR''' | | '''NOR''' | ||
| − | | [[Image: | + | | [[Image:nor.png|NOR symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 145: | Linia 181: | ||
|1 || 1 || 0 | |1 || 1 || 0 | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| '''XOR''' | | '''XOR''' | ||
| − | | [[Image: | + | | [[Image:xor.png|XOR symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 168: | Linia 200: | ||
|- | |- | ||
| '''XNOR''' | | '''XNOR''' | ||
| − | | [[Image: | + | | [[Image:xnor.png|XNOR symbol]] |
| − | |||
| | | | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
| Linia 187: | Linia 218: | ||
|} | |} | ||
| − | + | Ca și la reprezentarea simbolică a amplificatoarelor operaționale, se observă că nici porțile logice nu au reprezentate porturile de alimentare (Vdd și Vss), vizibile pe schema inversorului CMOS. Acestea se consideră implicit conectate la sursa de alimentare, respectiv la masă. | |
| − | + | == Verilog si SystemVerilog HDL == | |
| − | |||
| − | |||
| − | |||
| − | + | La ora actuală, un circuit digital poate ajunge până la 1 miliard de porți. Asta implică faptul că avem nevoie de unelte care să permită automatizarea procesului de design. Acest lucru se poate face folosind limbaje de descriere hardware ([http://en.wikipedia.org/wiki/Hardware_description_language Hardware Description Languages]). Aceste limbaje sunt special concepute pentru a putea descrie un circuit digital, ori din punct de vedere al comportamentului, ori din punct de vedere al structurii. În mod evident, o descriere comportamentală a unui circuit va fi mai succintă, dar nu va oferi informații despre structura dorită (la nivel de poartă), în timp ce o descriere structurală va fi mai exactă din punct de vedere al componentelor circuitului, dar mai lungă și poate mai dificil de înțeles. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | ) | ||
| − | + | Există două limbaje foarte cunoscute de descriere hardware: [http://en.wikipedia.org/wiki/Verilog Verilog] și [http://en.wikipedia.org/wiki/VHDL VHDL]. În continuarea acestui laborator de Circuite Integrate Digitale, vom folosi pentru descriere circuitelor, limbajul Verilog. Sintaxa acestuia este simplă și este parțial moștenită din C. Totuși, este foarte important de reținut că Verilog nu este un limbaj de programare. El nu se „execută” secvențial de către un procesor, ci se sintetizeaza într-un circuit sau se simulează. Prin urmare utilizatorii de Verilog trebuie să se dezobișnuiască să gândească secvențial ca și cum fiecare linie de cod se execută după cea precedentă, si mai degrabă trebuie să-și imagineze cum funcționează circuitul pe care codul respectiv îl descrie. Astfel, diferența cea mai interesantă față de un limbaj de programare, este că ordinea blocurilor de cod dintr-un modul nu contează. | |
| − | + | SystemVerilog este o completare la standardul de bază Verilog și aduce multe imbunătățiri în direcția verificării circuitelor, cum ar fi conceptele de programare orientată pe obiecte. Pe langă acestea, apar și câteva imbunătățiri menite să ajute procesul de proiectare, cum ar fi o diferența mai clară și mai usor de urmărit dintre circuitele combinaționale și secvențiale. | |
| − | |||
| − | + | Înainte de a începe lucrul cu uneltele software de simulare și sinteză, parcurgeți tutorial-ul care explică sintaxa [[SystemVerilog]]. | |
| − | [ | ||
Versiunea curentă din 20 februarie 2025 09:54
Introducere în Circuite Digitale
Semnale analogice
Începând cu lecțiile de electrocinetică de la orele de fizică din liceu (surse de tensiune, rezistențe, condensatoare, bobine, etc.) și terminând cu orele de Dispozitive și Circuite Electronice, sistemele studiate au fost formate din componente formând circuite analogice. Circuitele analogice sunt circuite în care mărimile studiate (curent, tensiune), variază continuu în anumite intervale. Un exemplu concret este un amplificator audio, care preia un semnal sonor analogic și îl amplifică pentru a putea fi transmis mai departe, la un sistem de boxe. Puteți vedea un exemplu de semnal analogic în figura alăturată. Desigur, această imagine este generată de un computer, care este un dispozitiv digital, astfel ea nu poate reprezenta un semnal analogic adevărat ci poate doar simula un astfel de semnal, cu o anumită precizie.
Semnale digitale
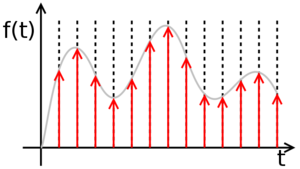
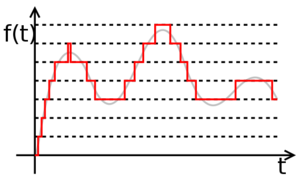
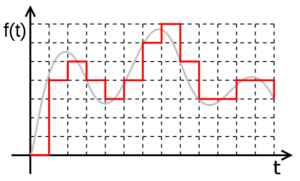
Un semnal digital este o înșiruire de valori discrete, fiecare din aceste valori făcând parte dintr-o mulțime discretă de valori raționale. Transformarea unui semnal analogic într-un semnal digital, implică o pierdere de precizie. Să luăm spre exemplu un semnal analogic sinusiodal simplu, reprezentând variația în timp a tensiunii la bornele unui rezistor. Între momentele t=0 și t=1, funcția, fiind continuă, are o infinitate de valori, prin urmare este imposibil de a izola fiecare valoare în parte, șirul astfel obținut fiind infinit. Procedura, în această situație, este de a izola doar o parte din valori, la anumite momente de timp, numite eșantioane, astfel încât să obținem un șir finit de valori. Această procedură se numește eșantionare, iar perioada de timp dintre două eșantioane succesive, poartă numele de perioadă de eșantionare. Cu cât perioada de eșantionare este mai mică (respectiv frecvența de eșantionare mai mare), cu atât semnalul digital obținut este o copie mai fidelă (pierdere mai mica de precizie) față de semnalul analogic original. Dacă totuși semnalul analogic este de bandă limitată (adică poate fi scris ca o sumă finită de semnale sinusoidale), atunci teorema eșantionării arată că dacă eșantionarea se face cu o frecvență de cel puțin de două ori mai mare decât frecvența maximă din spectrul semnalului, din seria de eșantioane se poate obține cu precizie de 100% semnalul analogic original.
Totuși, mai există o problemă. Semnalul fiind continuu, valorile eșantioanele se află într-un spațiu continuu, prin urmare de precizie infinită. Pentru a reduce precizia valorilor, se utilizează un procedeu numit cuantizare. Acest procedeu implică împărțirea intervalului de valori posibile pentru semnal în subdiviziuni. Cu cât aceste subdiviziuni sunt mai fine, cu atât valorile obținute prin cuantizare vor fi mai aproape de valorile reale ale semnalului original, dar vor fi reprezentate cu un număr mai pare de simboluri.
În concluzie, un semnal digital este o înșiruire de numere, obținute prin eșantionarea și cuantizarea unui semnal analogic.
Numere și simboluri. Baze de numerație
După cum s-a observat în capitolul anterior, un semnal digital este o înșiruire de valori. Aceste valori sunt reprezentate folosind simboluri, aparținând unei baze de numerație. Cel mai simplu exemplu este cel cu care suntem obișnuiți cu toții, adică baza zecimală, folosind ca simboluri cifrele de la 0 la 9. Dar acesta nu este nici pe departe singurul. Alte exemple ar fi sistemul de numerație roman, unde se folosesc ca simboluri literele I, V, X, L, C, D și M, unde valoarea acestor simboluri intr-un număr depinde de ordinea lor. Același lucru îl putem spune și despre baza de numerație zecimala, unde, spre exemplu, simbolul 9 are altă valoare dacă se află pe prima poziție (9) decât dacă se află pe a doua (90). Ce este interesant de reținut este că, în ciuda asocierii mentale dintre simbolurile cu care am fost obișnuiți de mici să lucrăm și valorile numerice pe care acestea le exprimă, cele două noțiuni sunt complet distincte. Valoarea „zece” poate fi exprimată numeric în baza zecimala ca 10, în sistemul de numerație roman ca X, în sistemul hexazecimal ca A, în sistemul binar ca 1010, în cel octal ca 12, dar toate aceste reprezentări exprimă, de fapt, același număr.
Sistemul de numerație binar
După cum îi spune și numele, acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 104, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza 2, un 1 pe pozitia 4 este echivalent cu valoarea 1 * 24. Aceasta este și regula de transformare a numerelor din baza 2 în baza 10. Prin urmare:
1001010(2) = 1 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 64 + 0 + 0 + 8 + 0 + 2 + 0 = 54(10)
Transformarea unui număr din baza zecimală în cea binară implică împărțirea repetată la 2 (numărul de simboluri ale bazei), unde deîmpărțitul la fiecare iterație este dat de câtul împărțirii anterioare. Operația se repetă cât timp câtul este diferit de 0. Numărul în baza binară este dat de secvența resturilor începând cu ultima împărțire și terminând cu prima.
Avantajul sistemului binar este că numărul redus de simboluri face ca și numărul de operații posibile între două simboluri aleatoare să fie redus, prin urmare este ușor de imaginat o realizare fizică a unor circuite care să implementeze aceste operații. Dezavantajul este că pentru numere relativ mici, este nevoie de multe simboluri pentru reprezentare. Așadar, pentru flexibilitatea operației cu valori reprezentate cu multe simboluri, se utilizeaza baza de numerație hexazecimală, adică baza 16. După cum îi spune și numele, baza hexazecimală utilizează 16 simboluri: cifrele de la 0 la 9, și caracterele a, b, c, d, e și f. Utilizarea bazei 16 este avantajoasă datorită trecerii foarte ușoare între ea și baza 2. Astfel, la orice valoare reprezentată printr-o secvență de patru simboluri binare corespunde unul și numai un simbol hexazecimal.
Computație și control
Am ajuns deci la concluzia că se pot face calcule (computație) folosind doar două simboluri, corespunzătoare valorilor de zero și de unu. Avem la dispoziție o bază de numerație (baza doi), prin care se pot face calcule din cele mai complexe, cu aceeași acuratețe ca și cele din baza decimală. Dar pe lângă calculul efectiv, un sistem informatic trebuie să poată lua decizii, adică să poate evalua o expresie și să decidă valoarea acesteia de adevăr, operație de tipul general if then else. Cel mai simplu exemplu de funcție care nu se poate calcula fără luarea unei decizii, este funcția modul (de fapt, orice funcție cu ramuri). Aceasta este de forma:
if (operand < 0) then (result = -operand) else (result = operand);
Expresia (operand < 0) este ceea ce se numește o expresie logică. Expresiile logice, în algebra booleană, pot lua numai două valori: adevărat sau fals. Aceste valori pot fi notate cu aceleași simboluri pe care le utilizăm pentru valori numerice în baza doi, adică 0 pentru valoarea de adevăr fals (false) și 1 pentru valoarea de adevăr adevărat (true).
Cum asupra valorilor numerice pot fi aplicați operatori numerici (adunare, scădere, înmulțire), și asupra valorilor logice, pot fi aplicați operatori logici (ȘI, SAU, NU, SAU EXCLUSIV). Aceștia sunt explicați în detaliu pe pagina Wikipedia a algebrei booleane.
Concluzia este că folosind aceleași două simboluri, putem face calcule, folosind algebra binară, dar putem exercita control asupra unei funcții, folosind algebra booleană. După cum simbolurile se suprapun pentru computație și control, și operatorii asociați pot avea aceeași formă, și atunci distincția se face doar prin interpretarea lor. Spre exemplu, tabelul cu rezultate pentru înmulțirea a două numere de un bit (operație numerică) arată în felul următor:
| INTRARE | IEȘIRE | |
| A | B | A * B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
În același timp, operația logică ȘI care întoarce 1 dacă și numai dacă ambii operanzi sunt 1 (mă duc la film DACĂ nu plouă ȘI am bani), are următorul tabel de adevăr:
| INTRARE | IEȘIRE | |
| A | B | A ȘI B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Se observă că cele două funcții sunt identice. În acest fel, distincția dintre valoare logică și valoare numerică (respectiv operator logic și operator numeric) ține de interpretarea valorilor de intrare (dacă acestea sunt valori logice sau numerice) iar implementarea operatorilor este identică (prin urmare circuitul asociat este identic).
Circuite
În electronica digitală, ca de fapt în toată ramura tehnologiei care lucrează cu circuite digitale (adică calculatoare) ca și în teroria informației, un element care poate lua o valoare binară asociată unui simbol binar, se numește bit. Baza circuitelor digitale, oricât de complexe, este dată de sub-circuitele care calculează operațiile unare și binare (adică care care au unul respectiv doi operanzi) între doi biți. Un astfel de sub-circuit se numește poartă (en:gate). Aceeași poartă poate fi considerată implementarea unui operator numeric de un bit, dar și implementarea unui operator logic.
Modul de codare a valorilor asociate simbolurilor binare, în electronica digitală, este printr-o diferență de potențial între două puncte. În tehnologia curentă utilizată (CMOS), o tensiune între 0 și Vdd/2 este asociată valorii binare de 0 iar o tensiune între Vdd/2 și Vdd valorii binare de 1.[1]
Cea mai simplă poartă este cea care implementează operația logică de negare (are o singură intrare și o singură ieșire care este intotdeauna diferită de cea de intrare, adică pentru intrarea 0, ieșirea este 1 și pentru intrarea 1, ieșirea este 0). Această poartă se numește inversor, sau poartă NU (en: inverter, NOT gate).
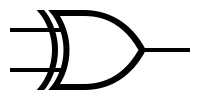
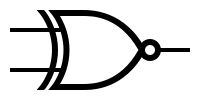
Simbolurile și tabelele de adevăr pentru cele mai utilizare porți:
Ca și la reprezentarea simbolică a amplificatoarelor operaționale, se observă că nici porțile logice nu au reprezentate porturile de alimentare (Vdd și Vss), vizibile pe schema inversorului CMOS. Acestea se consideră implicit conectate la sursa de alimentare, respectiv la masă.
Verilog si SystemVerilog HDL
La ora actuală, un circuit digital poate ajunge până la 1 miliard de porți. Asta implică faptul că avem nevoie de unelte care să permită automatizarea procesului de design. Acest lucru se poate face folosind limbaje de descriere hardware (Hardware Description Languages). Aceste limbaje sunt special concepute pentru a putea descrie un circuit digital, ori din punct de vedere al comportamentului, ori din punct de vedere al structurii. În mod evident, o descriere comportamentală a unui circuit va fi mai succintă, dar nu va oferi informații despre structura dorită (la nivel de poartă), în timp ce o descriere structurală va fi mai exactă din punct de vedere al componentelor circuitului, dar mai lungă și poate mai dificil de înțeles.
Există două limbaje foarte cunoscute de descriere hardware: Verilog și VHDL. În continuarea acestui laborator de Circuite Integrate Digitale, vom folosi pentru descriere circuitelor, limbajul Verilog. Sintaxa acestuia este simplă și este parțial moștenită din C. Totuși, este foarte important de reținut că Verilog nu este un limbaj de programare. El nu se „execută” secvențial de către un procesor, ci se sintetizeaza într-un circuit sau se simulează. Prin urmare utilizatorii de Verilog trebuie să se dezobișnuiască să gândească secvențial ca și cum fiecare linie de cod se execută după cea precedentă, si mai degrabă trebuie să-și imagineze cum funcționează circuitul pe care codul respectiv îl descrie. Astfel, diferența cea mai interesantă față de un limbaj de programare, este că ordinea blocurilor de cod dintr-un modul nu contează.
SystemVerilog este o completare la standardul de bază Verilog și aduce multe imbunătățiri în direcția verificării circuitelor, cum ar fi conceptele de programare orientată pe obiecte. Pe langă acestea, apar și câteva imbunătățiri menite să ajute procesul de proiectare, cum ar fi o diferența mai clară și mai usor de urmărit dintre circuitele combinaționale și secvențiale.
Înainte de a începe lucrul cu uneltele software de simulare și sinteză, parcurgeți tutorial-ul care explică sintaxa SystemVerilog.