Diferență între revizuiri ale paginii „CID aplicatii 7 : Circuite secventiale elementare”
Cbira (discuție | contribuții) (Modified: Verilog-> SystemVerilog (always_ff instead of always@ and always_comb instead of always@(*))) |
|||
| (Nu s-au afișat 9 versiuni intermediare efectuate de un alt utilizator) | |||
| Linia 18: | Linia 18: | ||
[[Fișier:Circuit comb hazard propagare.png | 400px]] | [[Fișier:Circuit comb hazard propagare.png | 400px]] | ||
| + | |||
| + | |||
| + | ==Atribuirea blocanta si non-blocanta== | ||
| + | Pentru ca simulatorul sa functioneze in mod corect si semnalele sa se modifice in simulare asa cum se modifica si in realitate este nevoie sa folosim atribuirea blocanta ( semnul "=") la circuite combinationale si atribuirea non-blocanta (semnul "<=") la circuite secventiale. | ||
| + | |||
| + | In mod uzual orice always combinational ( '''always_comb''' ) va folosi '''atribuirea blocanta ( = )''' si orice always pe ceas ( '''always_ff @(posedge clock)''' ) va folosi '''atribuirea non-blocanta ( <= )'''. | ||
| + | |||
| + | Diferenta dintre cele 2 atribuiri consta in modul in care simulatorul "executa" instructiunea de atribuire. La atribuirea blocanta se simuleaza linie cu linie, in ordinea in care acestea au fost scrise. La atribuirea non-blocanta se salveaza toti termenii din dreapta si se pun deodata (in acelasi pas de simulare) in termenii din stanga. Pentru a clarifica acest concept avem exemplul de mai jos: | ||
| + | |||
| + | <syntaxhighlight lang="Verilog"> | ||
| + | a = b; | ||
| + | b = a; | ||
| + | |||
| + | c <= d; | ||
| + | d <= c; | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | In primul caz, deoarece am folosit atribuirea blocanta, a ia valoarea lui b si apoi b ia valoarea lui a, care deja a devenit b deci concret b ramane pe loc si deci atat a cat si b vor avea aceasi valoare la final. | ||
| + | |||
| + | In al doilea caz, deoarece am folosit atribuirea non-blocanta, ce este in partea dreapta se transfera peste operanzii din stanga deodata, astfel c ia valoarea lui d si d ia valoarea lui c, la final avand loc o interschimbare. | ||
| + | |||
==Latch-ul== | ==Latch-ul== | ||
| Linia 65: | Linia 86: | ||
Pentru modulul de test, va trebui să alegem un timp de modificare a valorilor semnalelor mai mare decât timpul de propagare ales. Aici, vom folosi 1ns timp de propagare și 5ns timp de variație a intrărilor in testbench. | Pentru modulul de test, va trebui să alegem un timp de modificare a valorilor semnalelor mai mare decât timpul de propagare ales. Aici, vom folosi 1ns timp de propagare și 5ns timp de variație a intrărilor in testbench. | ||
| − | '''Implementarea | + | '''Implementarea SystemVerilog a circuitului''' |
<syntaxhighlight lang="Verilog"> | <syntaxhighlight lang="Verilog"> | ||
`timescale 1ns/1ps | `timescale 1ns/1ps | ||
module Circuit( | module Circuit( | ||
| − | input a, | + | input logic a, |
| − | input b, | + | input logic b, |
| − | output c, | + | output logic c, |
| − | output d | + | output logic d |
); | ); | ||
| Linia 88: | Linia 109: | ||
module Circuit_TB(); | module Circuit_TB(); | ||
| − | + | logic a_t, b_t; | |
| − | + | logic c_t, d_t; | |
initial begin | initial begin | ||
| Linia 107: | Linia 128: | ||
endmodule | endmodule | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| + | |||
| + | |||
| + | [[Fișier:Poza_hazard.png | 800px]] | ||
| + | |||
| + | In acest exemplu se observa ca iesirea c se modifica la 1ns dupa modificarile intrarilor (intarizerea adaugata pentru transmiterea prin porti) si iesirea d se modifica de 2 ori: prima data la 1ns din cauza intrarilor si a doua oara dupa inca 1ns din cauza lui c. In intervalul [6-7]ns apare o valoare parazita, un hazard. | ||
| + | |||
===Exemplul 2: Descrierea comportamentală a latch-ului de tip D=== | ===Exemplul 2: Descrierea comportamentală a latch-ului de tip D=== | ||
| − | '''Descrierea | + | '''Descrierea SystemVerilog a modulului''' |
<syntaxhighlight lang="Verilog"> | <syntaxhighlight lang="Verilog"> | ||
module latch_D( | module latch_D( | ||
| − | input D, | + | input logic D, |
| − | input E, | + | input logic E, |
| − | output Q | + | output logic Q |
); | ); | ||
| Linia 128: | Linia 155: | ||
module latch_D_TB(); | module latch_D_TB(); | ||
| − | + | logic D_t, E_t; | |
| − | + | logic Q_t; | |
initial begin | initial begin | ||
| Linia 152: | Linia 179: | ||
===Exemplul 3: Descrierea comportamentală a bistabilului de tip D=== | ===Exemplul 3: Descrierea comportamentală a bistabilului de tip D=== | ||
| − | '''Descrierea | + | '''Descrierea SystemVerilog a modulului''' |
<syntaxhighlight lang="Verilog"> | <syntaxhighlight lang="Verilog"> | ||
module flipflop_D( | module flipflop_D( | ||
| − | input data_in, | + | input logic data_in, |
| − | input clock, | + | input logic clock, |
| − | output | + | output logic data_out |
); | ); | ||
| − | + | always_ff @(posedge clock) begin | |
| − | data_out <= data_in; | + | data_out <= data_in; // atribuire non-blocanta |
end | end | ||
| Linia 173: | Linia 200: | ||
module flipflop_D_TB(); | module flipflop_D_TB(); | ||
| − | + | logic data_in_t, clock_t; | |
| − | + | logic data_out_t; | |
initial begin | initial begin | ||
| Linia 198: | Linia 225: | ||
'''Observatie:''' Atunci cand avem un circuit secvential, se foloseste atribuirea non-blocanta ("<=”) | '''Observatie:''' Atunci cand avem un circuit secvential, se foloseste atribuirea non-blocanta ("<=”) | ||
| − | |||
==Exerciții== | ==Exerciții== | ||
| Linia 218: | Linia 244: | ||
Realizați un modul de test care să respecte la generarea stimulilor forma de unda prezentată în secțiunea de introducere teoretică, la '''Bistabilul de tip D cu reset asincron'''. | Realizați un modul de test care să respecte la generarea stimulilor forma de unda prezentată în secțiunea de introducere teoretică, la '''Bistabilul de tip D cu reset asincron'''. | ||
| − | '''Indicație''': Frontul căzător | + | '''Indicație''': Frontul căzător al semnalului ''reset'' va trebui să fie adăugat în lista de sensitivități a blocului always care determină modificarea lui ''data_out''. |
| + | |||
| + | ===Exercițiul 4=== | ||
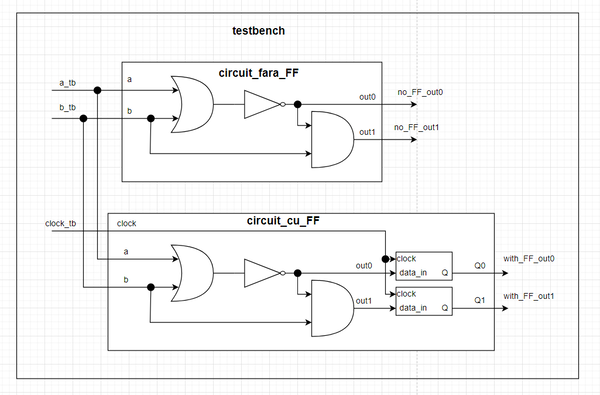
| + | Pentru evidentierea hazardului combinational (si a modului in care acesta se rezolva) descrieti in SystemVerilog si simulati urmatoarele 2 circuite: | ||
| + | |||
| + | [[Fișier:Poza_circ_secventiale_basic_exercitiu_4_circuit.png | 600px]] | ||
| + | |||
| + | Pentru a putea observa efectele hazardului, portile trebuie descrise ca avand timpi de propagare. | ||
| + | |||
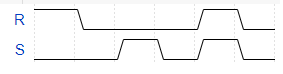
| + | Formele de unda pentru semnalele de la intrare vor fi: | ||
| + | |||
| + | [[Fișier:Poza_circ_secventiale_basic_exercitiu_4_forme_unda.png | 600px]] | ||
| + | |||
| + | ===Exercițiul 5=== | ||
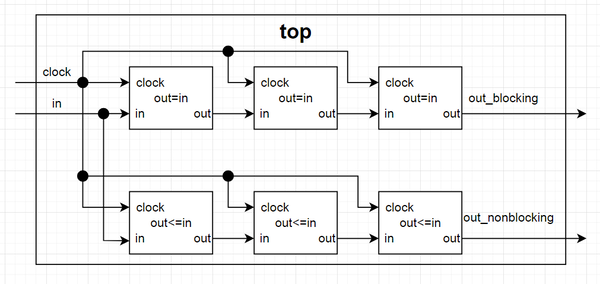
| + | Pentru evidentierea efectului atribuirii blocant si non-blocante se va implementa si simula circuitul de mai jos. El este alcatuit din 3 registre, fiecare memorand (si punand la iesire) pe frontul pozitiv al ceasului valoarea de la intrare. | ||
| + | |||
| + | Cele 3 registre de sus vor folosii atribuirea blocanta si cele 3 registre de jos vor folosii atribuirea non-blocanta. In simulare se doreste a se vizualiza: intrarile, iesirile, firele interne de legatura dintre registrii. | ||
| + | |||
| + | Pentru a scrie semnificativ mai putin, nu este nevoie sa instantiati fiecare registru dintro serie ca modul separat ci se pot face toate cele 3 atribuiri in cadrul aceluiasi bloc "always", la nivelul de top. Practic tot circuitul se reduce la un fisier de top ce contine intrari/iesiri, declararea registrilor pe 1b si cele 2 always-uri care dicteaza functionarea. | ||
| + | |||
| + | |||
| + | [[Fișier:Poza_circ_secventiale_basic_exercitiu_5_circuit.png | 600px]] | ||
Versiunea curentă din 9 aprilie 2025 06:56
Hazardul combinațional
Hazardul apare atunci când modificarea unei intrări a unui circuit combinațional determină modificări nedorite ale ieșirii. Aceste variații apar datorită diferențelor de întârzieri pe diverse căi de la intrare către ieșire.
De unde aceste întârzieri? Fiecare poartă este, așa cum am văzut la începutul aplicațiilor, un circuit electronic format, de obicei, din tranzistoare MOS. Răspunsul acestor dispozitive nu este instantaneu, introducând întârzieri. Timpul scurs de la modificarea unei intrări a unei porți până la modificarea corespunzătoare a ieșirii se numește timp de propagare.
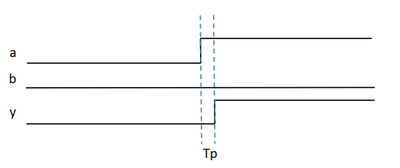
În figura următoare avem evidențiat timpul de propagare printr-o poartă SAU (Tp). Acesta este reprezentat de timpul scurs de la modificarea lui a până la modificarea ieșirii.
Avănd un circuit cu mai multe porți în cascadă, căile prin care anumite semnale ajung la intrările unei anumite porți pot diferi. Datorită timpilor de propagare diferiți care afectează aceste semnale până să ajungă la poarta curentă și a timpului de propagare efectiv al porții curente, pot apărea la ieșire tranziții nedorite ale semnalelor. Dacă la ieșire se așteaptă ca linia să rămană constant în 1, dar apare o scurtă tranziție prin 0, hazardul se numește 1 static. Dacă la ieșire se așteaptă ca linia să rămană constant în 0, dar apare o scurtă tranziție prin 1, hazardul se numește 0 static. Dacă se așteaptă o tranziție la ieșire, dar apare un regim tranzitoriu cu numeroase tranziții până la stabilizare, hazardul se numește dinamic.
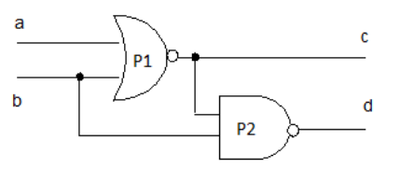
Pentru a înțelege mai bine, să considerăm exemplul de mai jos:
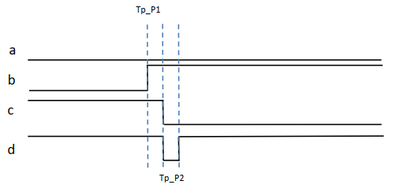
Observăm că intrările porții P2 urmează căi diferite: semnalul c este ieșirea unei porți, având o întârziere cauzată de timpul de propagare al porții P1, pe când semnalul b vine direct de la intrare, propagarea prin fir fiind neglijabilă. Să considerăm cazul în care intrarea a rămane permanent în 0, iar intrarea b comută la un moment dat din 0 în 1. Inițial, semnalul c este 1, iar d este 1. După comutarea lui b, semnalul c va comuta din 1 in 0, iar d va rămane 1. Acesta este cazul ideal. În realitate, datorită timpilor de propagare ai porților logice P1 și P2, vom avea o scurtă tranziție prin 0:
Atribuirea blocanta si non-blocanta
Pentru ca simulatorul sa functioneze in mod corect si semnalele sa se modifice in simulare asa cum se modifica si in realitate este nevoie sa folosim atribuirea blocanta ( semnul "=") la circuite combinationale si atribuirea non-blocanta (semnul "<=") la circuite secventiale.
In mod uzual orice always combinational ( always_comb ) va folosi atribuirea blocanta ( = ) si orice always pe ceas ( always_ff @(posedge clock) ) va folosi atribuirea non-blocanta ( <= ).
Diferenta dintre cele 2 atribuiri consta in modul in care simulatorul "executa" instructiunea de atribuire. La atribuirea blocanta se simuleaza linie cu linie, in ordinea in care acestea au fost scrise. La atribuirea non-blocanta se salveaza toti termenii din dreapta si se pun deodata (in acelasi pas de simulare) in termenii din stanga. Pentru a clarifica acest concept avem exemplul de mai jos:
a = b;
b = a;
c <= d;
d <= c;
In primul caz, deoarece am folosit atribuirea blocanta, a ia valoarea lui b si apoi b ia valoarea lui a, care deja a devenit b deci concret b ramane pe loc si deci atat a cat si b vor avea aceasi valoare la final.
In al doilea caz, deoarece am folosit atribuirea non-blocanta, ce este in partea dreapta se transfera peste operanzii din stanga deodata, astfel c ia valoarea lui d si d ia valoarea lui c, la final avand loc o interschimbare.
Latch-ul
Latch-urile sunt dispozitive elementare de memorare, sensibile la nivelul semnalelor de intrare. Exemple de astfel de dispozitive sunt latch-urile de tip SR și latch-urile de tip D.
Latch-ul SR
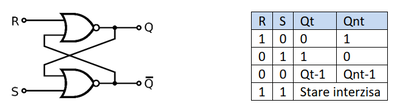
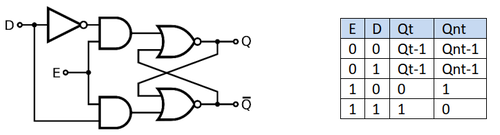
Latch-ul de tip SR poate fi realizat cu două porți SI NU sau SAU NU și este un dispozitiv asincron controlat de stările semnalelor S (set) și R (reset). Tabelul de adevăr al acestui circuit este prezentat mai jos.
Atunci când S este 1 și R este 0, ieșirea Q va deveni 1, iar Qn va deveni 0. Atunci când R este 1 și S este 0, ieșirea Q se resetează (devine 0), iar Qn devine 1. Starea de memorare apare atunci când atât R cât și S sunt 0 în același timp. Cazul în care R și S sunt 1 în același timp duce la un comportament nedorit. (atât Q cât și Qn vor fi 0, ceea ce este incorect din punct de vedere al logicii dorite – Qn să fie negatul lui Q). În plus, dacă din aceasta stare se dorește trecerea în starea de memorare (R = 0, S = 0), poate apărea oscilația. În realitate, cele două porți nu vor avea același timp de propagare datorită variațiilor de producție și circuitul va ajunge în cele din urma într-o stare stabilă, nepredictibilă.
Latch-ul de tip D
Latch-ul de tip D elimină problema combinațiilor nedorite de la ieșire. Acesta modifică ieșire doar atunci când semnalul de enable (E) este 1. Altfel, atunci când E este 0, va memora starea anterioara (Qt-1).
Bistabilul de tip D
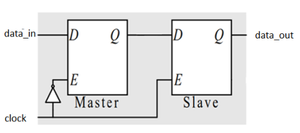
Bistabilul de tip D este un dispozitiv de memorare ce salvează valoarea intrării pe unul din fronturile ceasului (în mod uzual, frontul crescător). El poate fi obținut prin conectarea a două latch-uri de tip D, conform schemei de mai jos. De obicei, singura ieșire care ne interesează este Q.
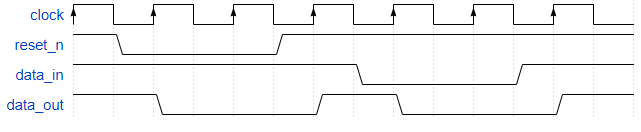
Comportamentul bistabilului de tip D poate fi observat în forma de undă următoare. Modificările lui data_out sunt determinate de fronturile crescătoare ale semnalului clock. La apariția acestora, data_out va lua valoarea intrării data_in.
Bistabilul de tip D cu reset sincron
Resetarea unui bistabil înseamnă aducerea valorii memorate la 0 sau la o altă valoare de reset definită de cel care proiectează circuitul. Vom considera în exemplul nostru că semnalul de reset va fi activ în 0 și va face 0 valoarea memorată atunci când este activ. Un reset sincron înseamnă că acesta va acționa asupra valorii memoratedata_out pe frontul crescător al ceasului.
Bistabilul de tip D cu reset asincron
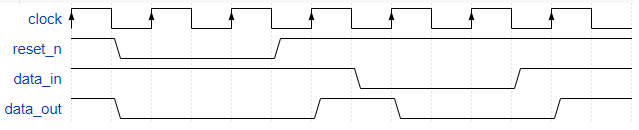
Un reset asincron înseamnă că acesta va acționa asincron, fără a ține cont de ceas. Acest lucru înseamnă că el va acționa asupra valorii memorate imediat ce devine activ. În exemplele noastre, vom considera semnalul de reset ca fiind activ în 0. Trecerea sa în 0 (frontul căzător) determină imediat resetarea circuitului. De asemenea, orice eveniment de front crescător de ceas ce apare cât timp reset-ul este activ, va duce la menținerea resetării circuitului.
Exemple
Exemplul 1: Evidențierea hazardului combinațional
Implementați circuitul cu porți logice prezentat în secțiunea de introducere teoretică și reproduceți în modulul de testare variațiile semnalelor a și b propuse, astfel încât să observăm pe ieșirea d hazardul.
Deoarece în simulare propagarea este ideală, va trebui să introducem un timp de propagare folosind #n. Acesta va avea efect doar în simulare și va fi ignorat la o eventuală sinteză.
Pentru modulul de test, va trebui să alegem un timp de modificare a valorilor semnalelor mai mare decât timpul de propagare ales. Aici, vom folosi 1ns timp de propagare și 5ns timp de variație a intrărilor in testbench.
Implementarea SystemVerilog a circuitului
`timescale 1ns/1ps
module Circuit(
input logic a,
input logic b,
output logic c,
output logic d
);
assign #1 c = ~(a | b);
assign #1 d = ~(c & b);
endmodule
Implementarea unui modul de test care să evidențieze hazardul
`timescale 1ns/1ps
module Circuit_TB();
logic a_t, b_t;
logic c_t, d_t;
initial begin
a_t = 0;
b_t = 0;
#5 b_t = 1;
#5 $stop();
end
Circuit DUT(
.a(a_t),
.b(b_t),
.c(c_t),
.d(d_t)
);
endmodule
In acest exemplu se observa ca iesirea c se modifica la 1ns dupa modificarile intrarilor (intarizerea adaugata pentru transmiterea prin porti) si iesirea d se modifica de 2 ori: prima data la 1ns din cauza intrarilor si a doua oara dupa inca 1ns din cauza lui c. In intervalul [6-7]ns apare o valoare parazita, un hazard.
Exemplul 2: Descrierea comportamentală a latch-ului de tip D
Descrierea SystemVerilog a modulului
module latch_D(
input logic D,
input logic E,
output logic Q
);
assign Q = (E == 1) ? D : Q;
endmodule
Modul de test pentru latch-ul D
`timescale 1ns/1ps
module latch_D_TB();
logic D_t, E_t;
logic Q_t;
initial begin
D_t = 0;
E_t = 1;
#1 D_t = 1;
#1 D_t = 0;
#1 E_t = 0;
#1 D_t = 1;
#1 D_t = 0;
#5 $stop();
end
latch_D DUT1(
.D(D_t),
.E(E_t),
.Q(Q_t)
);
endmodule
Exemplul 3: Descrierea comportamentală a bistabilului de tip D
Descrierea SystemVerilog a modulului
module flipflop_D(
input logic data_in,
input logic clock,
output logic data_out
);
always_ff @(posedge clock) begin
data_out <= data_in; // atribuire non-blocanta
end
endmodule
Modulul de test pentru bistabilul de tip D
`timescale 1ns/1ps
module flipflop_D_TB();
logic data_in_t, clock_t;
logic data_out_t;
initial begin
data_in_t = 0;
#2 data_in_t = 1;
#4 data_in_t = 0;
#5 $stop();
end
initial begin
clock_t = 0;
forever #1 clock_t = ~ clock_t;
end
flipflop_D DUT(
.data_in(data_in_t),
.clock(clock_t),
.data_out(data_out_t)
);
endmodule
Observatie: Atunci cand avem un circuit secvential, se foloseste atribuirea non-blocanta ("<=”)
Exerciții
Exercițiul 1
Descrieți structural latch-ul de tip SR, conform schemei din secțiunea de introducere teoretică. Puteți simula întârzierile prin porți folosind #1.
Realizați un modul de test care să pună în evidență funcționarea. Respectați la generarea stimulilor următoarea variație (fiecare segment de timp durează 5ns).
Exercițiul 2
Modificați descrierea bistabilului de tip D prezentată în exemple, astfel încât acesta să permită resetarea sincronă. Semnalul de reset va fi activ în 0.
Realizați un modul de test care să respecte la generarea stimulilor forma de unda prezentată în secțiunea de introducere teoretică, la Bistabilul de tip D cu reset sincron.
Exercițiul 3
Modificați descrierea bistabilului de tip D prezentată în exemple, astfel încât acesta să permită resetarea asincronă. Semnalul de reset va fi activ în 0.
Realizați un modul de test care să respecte la generarea stimulilor forma de unda prezentată în secțiunea de introducere teoretică, la Bistabilul de tip D cu reset asincron.
Indicație: Frontul căzător al semnalului reset va trebui să fie adăugat în lista de sensitivități a blocului always care determină modificarea lui data_out.
Exercițiul 4
Pentru evidentierea hazardului combinational (si a modului in care acesta se rezolva) descrieti in SystemVerilog si simulati urmatoarele 2 circuite:
Pentru a putea observa efectele hazardului, portile trebuie descrise ca avand timpi de propagare.
Formele de unda pentru semnalele de la intrare vor fi:
Exercițiul 5
Pentru evidentierea efectului atribuirii blocant si non-blocante se va implementa si simula circuitul de mai jos. El este alcatuit din 3 registre, fiecare memorand (si punand la iesire) pe frontul pozitiv al ceasului valoarea de la intrare.
Cele 3 registre de sus vor folosii atribuirea blocanta si cele 3 registre de jos vor folosii atribuirea non-blocanta. In simulare se doreste a se vizualiza: intrarile, iesirile, firele interne de legatura dintre registrii.
Pentru a scrie semnificativ mai putin, nu este nevoie sa instantiati fiecare registru dintro serie ca modul separat ci se pot face toate cele 3 atribuiri in cadrul aceluiasi bloc "always", la nivelul de top. Practic tot circuitul se reduce la un fisier de top ce contine intrari/iesiri, declararea registrilor pe 1b si cele 2 always-uri care dicteaza functionarea.