Diferență între revizuiri ale paginii „CID aplicatii 11 : Automate finite”
| (Nu s-au afișat 4 versiuni intermediare efectuate de același utilizator) | |||
| Linia 51: | Linia 51: | ||
//registrul de stare | //registrul de stare | ||
| − | always_ff@(posedge clock) begin | + | always_ff @(posedge clock) begin |
if(reset == 1) | if(reset == 1) | ||
state <= STATE_READ1; | state <= STATE_READ1; | ||
| Linia 97: | Linia 97: | ||
initial begin | initial begin | ||
| − | in_t = 1; | + | in_t <= 1; |
| − | reset_t = 1; | + | reset_t <= 1; |
| − | #2 reset_t = 0; | + | #2 reset_t <= 0; |
| − | #10 in_t = 0; | + | #10 in_t <= 0; |
| − | #10 in_t = 1; | + | #10 in_t <= 1; |
#10 $stop(); | #10 $stop(); | ||
end | end | ||
| Linia 143: | Linia 143: | ||
logic [1:0] state, state_next; | logic [1:0] state, state_next; | ||
| − | always_ff@(posedge clock) begin | + | always_ff @(posedge clock) begin |
if(reset == 1) | if(reset == 1) | ||
state <= Q0; | state <= Q0; | ||
| Linia 183: | Linia 183: | ||
localparam stare_wait_0 = 1'b1; | localparam stare_wait_0 = 1'b1; | ||
| − | logic | + | logic state, state_next; |
| − | always_ff@(posedge clock) begin | + | always_ff @(posedge clock) begin |
if(reset == 1) | if(reset == 1) | ||
state <= stare_wait_1; | state <= stare_wait_1; | ||
| Linia 201: | Linia 201: | ||
if(in == 0) state_next = stare_wait_1; | if(in == 0) state_next = stare_wait_1; | ||
end | end | ||
| − | default: state_next = | + | default: state_next = stare_wait_1 ; |
endcase | endcase | ||
end | end | ||
| Linia 226: | Linia 226: | ||
initial begin | initial begin | ||
| − | in_t = 0; | + | in_t <= 0; |
| − | reset_t = 1; | + | reset_t <= 1; |
| − | #2 reset_t = 0; | + | #2 reset_t <= 0; |
| − | #10 in_t = 1; | + | #10 in_t <= 1; |
| − | #5 in_t = 0; | + | #5 in_t <= 0; |
| − | #10 in_t = 1; | + | #10 in_t <= 1; |
| − | #5 in_t = 0; | + | #5 in_t <= 0; |
#10 $stop(); | #10 $stop(); | ||
end | end | ||
Versiunea curentă din 16 mai 2025 09:25
Automate finite
Automatul finit este folosit pentru a descrie sisteme ce tranziteaza un numar finit de stari. Acest tip de sistem este foarte util atunci cand starile nu sunt tranzitate intr-un mod simplu, evident sau repetitiv.
Automatul finit, numit și FSM (Finite State Machine), este un model matematic de computație, definit de următoarele elemente:
- O mulțime finită de simboluri de intrare, numită alfabet de intrare;
- O mulțime finită și nevidă de simboluri de ieșire, numită alfabet de ieșire;
- O mulțime finită și nevidă de stări, din care doar una, numită starea curentă, este activă la un moment dat;
- O stare inițială, care face parte din mulțimea stărilor;
- O funcție de tranziție a stărilor, care calculează starea următoare a automatului în funcție de starea curentă și de simbolul de intrare;
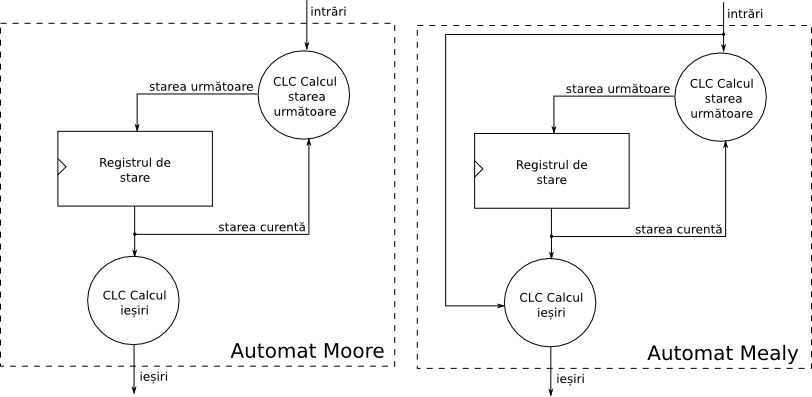
- O funcție de calcul a ieșirii, care determină simbolul de ieșire în funcție de starea curentă (în cazul automatelor de tip Moore) sau în funcție de starea curentă și de simbolul de intrare (în cazul automatelor de tip Mealy).
La fiecare front al ceasului, valoarea stării următoare, calculată de către CLC, va fi încărcată în registru. Dacă registrul are n biți, numărul maxim de stări care pot fi reprezentate este 2n. Acest număr poate fi mai mic, în funcție de schema de codare a stărilor. De exemplu, pentru n = 4, folosind codarea binară se pot reprezenta cel mult 16 stări (0000, 0001, 0010, ..., 1111), în timp ce pentru codarea one-hot, în care doar un singur bit poate lua valoarea 1, se pot reprezenta 4 stări (1000, 0100, 0010, 0001).
Pentru a reprezenta comportamentul unui automat finit, putem folosi grafuri sau organigrame, conventiile de notare depinzand de tipul automatului (Moore sau Mealy).
Exemple
Exemplul 1: Automat ce detecteaza secvente de tipul 11....100....0
In acest exemplu va fi implementat un automat care detecteaza secventele de tipul 11....100....0. Pentru aceasta, automatul va avea o intrare pe un bit (in, pe care va veni secventa de biti) si doua iesiri: detectOk, care semnalizeaza prin 1 ca nu a fost inca detectata o secventa ilegala si detectFail, care semnalizeaza prin 1 ca a fost detectata o secventa ilegala (un 1 dupa 0).
Automatul va avea 3 stari:
- Q0 - STATE_READ1: automatul intra in aceasta stare la reset si va ramane in aceasta atata timp cat intrarea este 1 (inca nu a aparut niciun 0).
- Q1 - STATE_READ0: automatul intra in aceasta stare atunci cand apare pe intrare primul 0 si va ramane in aceasta atata timp cat pe intrare este 0.
- Q2 - STATE_ERROR: automatul intra in aceasta stare atunci cand apare un 1 dupa 0 si va ramane blocat aici pana la reset.
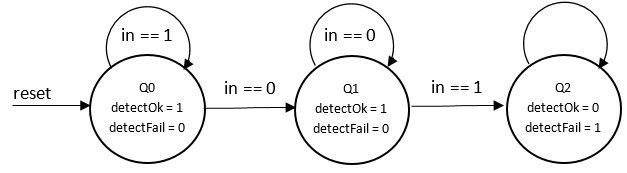
Pentru a coda cele 3 stari avem nevoie de minim 2 biti: STATE_READ1 = 2'b00, STATE_READ0 = 2'b01, STATE_ERROR = 2'b10.
Graful automatului este:
Implementarea automatului
module FSM1(
input logic clock,
input logic in,
input logic reset,
output logic detectOk,
output logic detectFail
);
//Se asociaza sirurilor de biti folositi pentru codarea starilor nume ce pot fi folosite mai usor in cod.
//La compilare, numele vor fi inlocuite in cod cu numerele asociate la inceput.
localparam STATE_READ1 = 2'b00;
localparam STATE_READ0 = 2'b01;
localparam STATE_ERROR = 2'b10;
logic [1:0] state, state_next;
//registrul de stare
always_ff @(posedge clock) begin
if(reset == 1)
state <= STATE_READ1;
else
state <= state_next;
end
//circuit combinational pentru calculul starii urmatoare
always_comb begin
state_next = state;
case(state)
STATE_READ1: begin
if(in == 0) state_next = STATE_READ0;
end
STATE_READ0: begin
if(in == 1) state_next = STATE_ERROR;
end
STATE_ERROR: state_next = STATE_ERROR;
default: state_next = STATE_READ1;
endcase
end
//circuit combinational pentru calculul iesirilor
assign detectOk = (state == STATE_READ0) || (state == STATE_READ1);
assign detectFail = (state == STATE_ERROR);
endmodule
Implementarea unui modul de test pentru FSM1
module FSM1_TB();
logic clock_t;
logic reset_t;
logic in_t;
logic detectOk_t;
logic detectFail_t;
initial begin
clock_t = 0;
forever #1 clock_t = ~clock_t;
end
initial begin
in_t <= 1;
reset_t <= 1;
#2 reset_t <= 0;
#10 in_t <= 0;
#10 in_t <= 1;
#10 $stop();
end
FSM1 DUT(
.clock(clock_t),
.reset(reset_t),
.in(in_t),
.detectOk(detectOk_t),
.detectFail(detectFail_t)
);
endmodule
Exemplul 2: Automat ce detecteaza fronturile crescatoare ale unui semnal
Automatul ce detecteaza fronturile crescatoare are un singur semnal de intrare in, care reprezinta semnalul analizat si o singura iesire, out, generand pe aceasta un puls lung cat o perioada de ceas la fiecare aparitie a unui front crescator pe in.
Vom avea nevoie de 3 stari:
- Q0: automatul intra in aceasta stare la reset si va ramane in aceasta atata timp cat intrarea este 0 (inca nu a aparut niciun front crescator).
- Q1: automatul intra in aceasta stare atunci cand apare pe intrare un front crescator. Dupa aparitia frontului crescator sunt doua posibilitati: linia ramane in 1, ceea ce duce la trecerea in starea Q2 care va duce iesirea in 0 dupa o perioada de ceas, sau linia trece in 0 dupa un ciclu de ceas, ceea ce duce la revenirea in starea Q0.
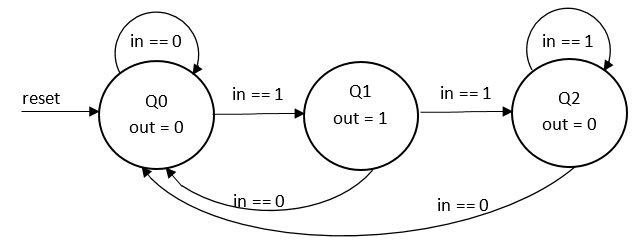
- Q2: automatul intra in aceasta stare atunci cand linia de intrare ramane in 1 mai mult de o perioada de ceas. Automatul va ramane in aceasta stare atata timp cat in ramane in 1 si va reveni in starea Q0 imediat ce in revine in 0.
Graful automatului este:
Implementarea automatului
module FSM2_Moore(
input logic clock,
input logic in,
input logic reset,
output logic out
);
localparam Q0 = 2'b00;
localparam Q1 = 2'b01;
localparam Q2 = 2'b10;
logic [1:0] state, state_next;
always_ff @(posedge clock) begin
if(reset == 1)
state <= Q0;
else
state <= state_next;
end
always_comb begin
state_next = state;
case(state)
Q0: begin
if(in == 1) state_next = Q1;
end
Q1: begin
if(in == 0) state_next = Q0;
if(in == 1) state_next = Q2;
end
Q2: begin
if(in == 0) state_next = Q0;
end
default: state_next = Q0;
endcase
end
assign out = (state == Q1); // iesirea depinde numai de stare => Moore
endmodule
module FSM2_mealy(
input logic clock,
input logic in,
input logic reset,
output logic out
);
localparam stare_wait_1 = 1'b0;
localparam stare_wait_0 = 1'b1;
logic state, state_next;
always_ff @(posedge clock) begin
if(reset == 1)
state <= stare_wait_1;
else
state <= state_next;
end
always_comb begin
state_next = state;
case(state)
stare_wait_1: begin
if(in == 1) state_next = stare_wait_0;
end
stare_wait_0: begin
if(in == 0) state_next = stare_wait_1;
end
default: state_next = stare_wait_1 ;
endcase
end
// daca pana acum semnalul a fost "0" si astept sa vina "1" si intrarea chiar vine "1" => am avut front crescator
assign out = (state==stare_wait_1) & (in==1); // in apare aici => dependenta iesiri de intrare => Mealy
endmodule
Implementarea unui modul de test pentru FSM2
module FSM2_TB();
logic clock_t;
logic reset_t;
logic in_t;
logic out_t;
initial begin
clock_t = 0;
forever #1 clock_t = ~clock_t;
end
initial begin
in_t <= 0;
reset_t <= 1;
#2 reset_t <= 0;
#10 in_t <= 1;
#5 in_t <= 0;
#10 in_t <= 1;
#5 in_t <= 0;
#10 $stop();
end
FSM2_Moore DUT(
.clock(clock_t),
.reset(reset_t),
.in(in_t),
.out(out_t)
);
endmodule
Se poate observa ca automatele de tip Moore au un numar mai mare de stari iar automatele de tip Mealy au o logica mai complexa pentru calcularea iesirilor.
Exerciții
Exercițiul 1
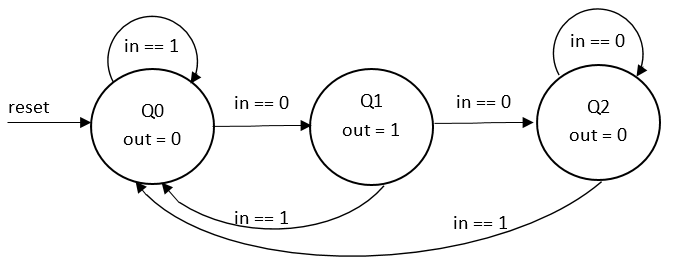
Implementați un automat finit ce detectează fronturile descrescătoare. Acesta are un singur semnal de intrare in, care reprezintă semnalul analizat și o singură ieșire out, generând pe această un puls lung cât o perioadă de ceas la fiecare apariție a unui front descrescător pe in.
Realizați implementarea SystemVerilog plecând de la graful automatului:
Exercițiul 2
Implementați un automat finit ce detectează atât fronturile crescătoare, cât și pe cele descrescătoare.
Exercițiul 3
Să se implementeze un circuit care generează un semnal PWM cu un factor de umplere ce variază triungular, la fiecare front descrescător al unui semnal de intrare.
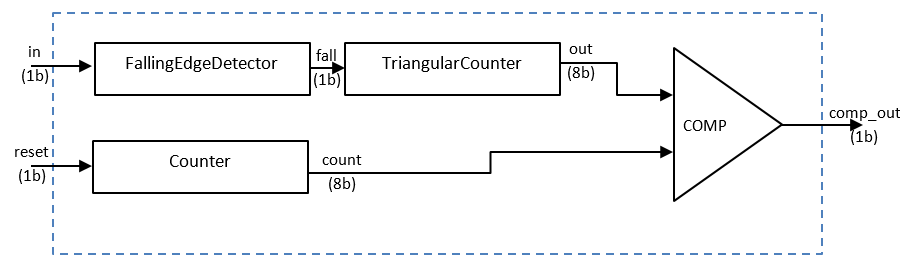
Schema circuitului este:
Modulele componente ale circuitului sunt:
- FallingEdgeDetector: Automat ce detectează fronturile descrescătoare ale semnalului de intrare.
- TriangularCounter: Automat ce generează la iesire secvența de numere 64, 128, 192, 255, 192, 128, 64.
- Counter: Numărător pe 8 biți cu reset sincron.
- COMP: Comparator cu două intrări pe 8 biți. Ieșirea sa va fi 1 atunci când counter < out și 0 în rest.
Exercițiul 4
Implementați automatul de control al unui aparat care vinde ciocolata.
O cafea costa 2.5 lei. Automatul accepta monezi de 50 de bani si hartii de 1 leu. Daca se depaseste suma, restul ramane in aparat si va fi folosit la urmatoarea tranzactie. Se accepta introducerea si a unei monezi si a unei bancnote in acelasi timp.
Intrarile sistemului sunt: clock (1b), reset (1b), in_50_b (1b), in_100_b (1b); iesirile sistemului sunt: give_cioco(1b).
Implementati automatul de control care va tine minte suma curenta si va da sau nu ciocolata in functie de aceasta. Implementati acest automat in ambele variante: Mealy si Moore.