Diferență între revizuiri ale paginii „Introduction. Verilog HDL (Verilog syntax)”

De la WikiLabs
Jump to navigationJump to search
Linia 1: Linia 1:
 
== Introduction to Digital Circuits ==
 
== Introduction to Digital Circuits ==
  
−
[[Fișier:Analogic_sig.png|thumb|Analog signal]]
+
[[File: Analogic_sig.png | thumb | Analog Sign]]
  
−
=== Analog signals ===
+
=== Analog Signals ===
  
−
Starting with the classes of electrocinetics of the physics in highschool (power supplies, resistors, capacitors, inductors, etc.) and ending with the classes of [[Dispozitive și Circuite Electronice]], the systems studied were formed by analog components. The analog circuits are circuits where the studied quantity (current, voltage), vary continuously in some intervals. An example would be an audio amplifier which gets the analog sound signal and amplifies it so that it is further sent to the speakers. One may see an example of analog signal in the side figure. Of course, this image generated on a computer (which is a digital device) cannot be represented by a true analog signalm but can only simulates such a signal, with a certain precision.
+
Starting with electro-kinetics lessons from high school physics classes (voltage sources, resistors, capacitors, coils, etc.) and ending with [[Electronic Devices and Circuits]], the studied systems were made up of analogue circuit components . Analog circuits are circuits in which the studied quantities (current, voltage) vary continuously at certain intervals. A concrete example is an audio amplifier that picks up an analog audio signal and amplifies it to be transmitted further to a speaker system. You can see an example of an analog signal in the figure below. Of course, this image is generated by a computer, which is a digital device, so it can not represent a true analog signal but can only simulate such a signal with some precision.
  
−
=== Digital signals ===
+
=== Digital Signals ===
  
−
[[Fișier:Sampled.signal.svg|thumb|Sampled signal (discrete in time, and with continuous values)]]
+
[[File: Sampled.signal.svg | thumb | Sample signal (discreet in time with continuous values)]]
−
[[Fișier:Quantized.signal.svg|thumb|Quantized signal (continuous in time and discrete in values)]]
+
[[File: Quantized.signal.svg | thumb | Quantized signal (continuous time with discrete values)]]
−
[[Fișier:Digital.signal.svg|thumb|Digital signal (quantized and sampled)]]
+
[[File: Digital.signal.svg | thumb | Digital signal (quantized and sampled)]]
  
−
A digital signal is a number of discrete values, each of them being part of a discrete set of rational values. Transforming an analog signal into a digital signal implies a loss of precision. Let's take for example a simple analog sine signal, representing the variation over time, of a voltage across a resistor. At moments t=0 and t=1, the function, being continuous, has an infinity of values, therefore, it is impossible to isolate each value, the resulting series being infinite. The procedure, in this situation, is to isolate just a part of the values, at certain moments in time, called "samples", so that we may get a finite series of values. This procedure is called [http://en.wikipedia.org/wiki/Sampling_(signal_processing) sampling], anf the time between two consecutive samples is called "sampling period". The shorter the sampling period (higher sampling frequency), the more accurate is the digital signal as a copy of the original analog singal (lower loss of precision). If however the analog signal has limited bandwidth (this means it can be written as a finite sum of sine signals), then, [http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem Sampling Theorem ] proves that if the sampling is performed with a frequency at least double the maxium frequency in the signal's spectrum, from the series of samples one can recover with 100% precision, the original analog signal.
+
A digital signal is a set of discrete values, each of these values ​​being part of a discrete set of rational values. Transforming an analog signal into a digital signal implies a loss of precision. Let's take for example a simple sinusoidal analog signal, representing the time variation of the voltage at the terminals of a resistor. Between the moments t = 0 and t = 1, the function, being continuous, has an infinity of values, so it is impossible to isolate each value, the sequence thus obtained being infinite. The procedure, in this situation, is to isolate only some of the values, at certain times, called samples, so that we get a finite set of values. This procedure is called [http://en.wikipedia.org/wiki/Sampling_(signal_processing) sampling] and the time period between two successive samples is called the sampling period. The shorter the sampling period (or the higher sampling frequency), the better the digital signal is a more accurate copy (lower precision loss) than the original analog signal. If, however, the analog signal is limited bandwidth (ie it can be written as a finite sum of sinusoidal signals), then [http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem sampling theorem] shows that if the sampling is done at a frequency at least twice as high as the maximum frequency of the signal spectrum, of the sample series can be obtained with 100% accuracy of the original analog signal.
  
−
Yet, there is another problem. The continuos signal has samples belonging to a continuous space, therefore of infinite precision. To transform it to discrete, one must reduce the precision of the values; the procedure used is called [http://en.wikipedia.org/wiki/Quantization_(signal_processing) quantization]. This procedure implies splitting the interval of possible values, in a finite number of subdivisions. The finer the subdivisions, the closer the resulting values are to the original values (the tradeoff will be that more simbols will be needed to express each subdivision)
 
  
−
To conclude, a digital signal is a series of numbers, obtained by sampling and quantizating an analog signal.
+
However, there is still a problem. The signal being continuous, the sample values ​​are in a continuous space, therefore of infinite precision. To reduce the accuracy of values, use a method called [http://en.wikipedia.org/wiki/Quantization_(signal_processing) quantization]. This process involves dividing the range of possible signal values ​​into subdivisions. The more subtle these subdivisions, the higher the values ​​obtained by the quantization will be closer to the real values ​​of the original signal, but will be represented by a more number of symbols.
  
−
=== Numbers and symbols. [http://en.wikipedia.org/wiki/Numeral_system Radix] ===
 
  
−
As seen in the previous chapter, a digital signal is a series of values.  
+
In conclusion, a digital signal is a sequence of numbers obtained by sampling and quantization of an analog signal.
  
−
După cum s-a observat în capitolul anterior, un semnal digital este o înșiruire de valori. Aceste valori sunt reprezentate folosind simboluri, aparținând unei baze de numerație. Cel mai simplu exemplu este cel cu care suntem obișnuiți cu toții, adică baza zecimală, folosind ca simboluri cifrele de la 0 la 9. Dar acesta nu este nici pe departe singurul. Alte exemple ar fi sistemul de numerație roman, unde se folosesc ca simboluri literele I, V, X, L, C, D și M, unde valoarea acestor simboluri intr-un număr depinde de ordinea lor. Același lucru îl putem spune și despre baza de numerație zecimala, unde, spre exemplu, simbolul 9 are altă valoare dacă se află pe prima poziție (9) decât dacă se află pe a doua (90). Ce este interesant de reținut este că, în ciuda asocierii mentale dintre simbolurile cu care am fost obișnuiți de mici să lucrăm și valorile numerice pe care acestea le exprimă, cele două noțiuni sunt complet distincte. Valoarea „zece” poate fi exprimată numeric în baza zecimala ca 10, în sistemul de numerație roman ca X, în sistemul hexazecimal ca A, în sistemul binar ca 1010, în cel octal ca 12, dar toate aceste reprezentări exprimă, de fapt, același număr.
+
=== Numbers and symbols. [http://en.wikipedia.org/wiki/Numeral_system Numbering Bases] ===
  
−
==== Sistemul de numerație binar ====
+
As noted in the previous chapter, a digital signal is a string of values. These values ​​are represented by symbols, belonging to a numbering base. The simplest example is the one we are all accustomed to, that is, the decimal point, using the figures from 0 to 9 as symbols. But this is by no means the only one. Other examples would be the Roman numeration system where symbols I, V, X, L, C, D, and M are used as symbols, where the value of these symbols in a number depends on their order. The same can be said about the decimal numbering base where, for example, the symbol 9 has another value if it is in the first position (9) than if it is on the second (90). What is interesting to note is that, despite the mental association between the symbols we have been used to working with and the numerical values ​​they express, the two notions are completely distinct. The value "ten" can be expressed numerically in the decimal number as 10 in the Roman numeration system as X in the hexadecimal system as A in the binary system as 1010 in the octal as 12 but all these representations actually express the same number.
  
−
După cum îi spune și numele, acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 10<sup>4</sup>, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza 2, un 1 pe pozitia 4 este echivalent cu valoarea 1 * 2<sup>4</sup>. Aceasta este și regula de transformare a numerelor din baza 2 în baza 10. Prin urmare:
+
==== Binary numbering system ====
  
−
1001010<sub>(2)</sub> = 1 * 2<sup>6</sup> + 0 * 2<sup>5</sup> + 0 * 2<sup>4</sup> + 1 * 2<sup>3</sup> + 0 * 2<sup>2</sup> + 1 * 2<sup>1</sup> + 0 * 2<sup>0</sup> = 64 + 0 + 0 + 8 + 0 + 2 + 0 = 54<sub>(10)</sub>
+
As the name says, this system uses only two symbols, most of them being 0 and 1. Therefore, a number can be represented in the binary system (also called base 2) as a sequence of 0 and 1 The order of the symbols in a written number in the second base follows the same rules as the numbers written in the decimal. Thus, if in a decimal number, the number 7 in position 4 was equivalent to 7 * 10 <sup> 4 </ sup>, where 10 is equal to the number of distinct symbols used, then to base 2, 4 is equivalent to 1 * 2 <sup> 4 </ sup>. This is also the rule for converting the numbers from base 2 to base 10. Therefore:
  
−
Transformarea unui număr din baza zecimală în cea binară implică împărțirea repetată la 2 (numărul de simboluri ale bazei), unde deîmpărțitul la fiecare iterație este dat de câtul împărțirii anterioare. Operația se repetă cât timp câtul este diferit de 0. Numărul în baza binară este dat de secvența resturilor începând cu ultima împărțire și terminând cu prima.
+
1001010 <sub> (2) </ sub> = 1 * 2 <sup> 6 </ sup> + 0 * 2 <sup> 3 </ sup> + 0 * 2 <sup> 2 </ sup> 0 + 8 + 0 + 2 + 0 = 54 <sub> (10) </ sub>
  
−
Avantajul sistemului binar este că numărul redus de simboluri face ca și numărul de operații posibile între două simboluri aleatoare să fie redus, prin urmare este ușor de imaginat o realizare fizică a unor circuite care să implementeze aceste operații. Dezavantajul este că pentru numere relativ mici, este nevoie de multe simboluri pentru reprezentare. Așadar, pentru flexibilitatea operației cu valori reprezentate cu multe simboluri, se utilizeaza baza de numerație hexazecimală, adică baza 16. După cum îi spune și numele, baza hexazecimală utilizează 16 simboluri: cifrele de la 0 la 9, și caracterele a, b, c, d, e și f. Utilizarea bazei 16 este avantajoasă datorită trecerii foarte ușoare între ea și baza 2. Astfel, la orice valoare reprezentată printr-o secvență de patru simboluri binare corespunde unul și numai un simbol hexazecimal.
+
Transforming a number from the decimal to the binary involves the repeated division into 2 (the number of base symbols), where the split at each iteration is given by the previous division. The operation is repeated as long as it is different than 0. The binary number is given by the remainder sequence from the last division to the first.
  
−
=== Computație și control ===
+
The advantage of the binary system is that the reduced number of symbols makes the number of possible operations between two random symbols reduced, so it is easy to imagine a physical realization of some circuits to implement these operations. The disadvantage is that for relatively small numbers, many symbols are needed for representation. Therefore, for the flexibility of the operation with values ​​represented by many symbols, the hexadecimal numbering base is used, ie the base 16. As the name says, the hexadecimal base uses 16 symbols: the digits 0 to 9, and the characters a, b, c d, e and f. The use of base 16 is advantageous due to the very slight passage between it and base 2. Thus, at any value represented by a sequence of four binary symbols, one and only one hexadecimal symbol corresponds.
  
−
Am ajuns deci la concluzia că se pot face calcule (computație) folosind doar două simboluri, corespunzătoare valorilor de zero și de unu. Avem la dispoziție o bază de numerație (baza doi), prin care se pot face calcule din cele mai complexe, cu aceeași acuratețe ca și cele din baza decimală. Dar pe lângă calculul efectiv, un sistem informatic trebuie să poată lua decizii, adică să poate evalua o expresie și să decidă valoarea acesteia de adevăr, operație de tipul general '''if then else'''. Cel mai simplu exemplu de funcție care nu se poate calcula fără luarea unei decizii, este funcția modul (de fapt, orice funcție cu ramuri). Aceasta este de forma:
+
=== Computation and control ===
−
<syntaxhighlight lang="Pascal">
 
−
if (operand < 0) then (result = -operand) else (result = operand);
 
−
</syntaxhighlight>
 
  
−
Expresia (operand < 0) este ceea ce se numește o expresie logică. Expresiile logice, în [http://en.wikipedia.org/wiki/Boolean_algebra algebra booleană], pot lua numai două valori: '''''adevărat''''' sau '''''fals'''''. Aceste valori pot fi notate cu aceleași simboluri pe care le utilizăm pentru valori numerice în baza doi, adică '''''0''''' pentru valoarea de adevăr '''''fals (false)''''' și '''''1''''' pentru valoarea de adevăr '''''adevărat (true)'''''.
+
We have therefore come to the conclusion that calculations can be made using only two symbols corresponding to zero and one. We have a numbering base (base two) that can be used to make the most complex calculations with the same accuracy as the decimal ones. But besides the actual calculation, a computer system must be able to make decisions, that is to say, to evaluate an expression and decide its value of truth, a general type of operation 'if' else ''. The simplest example of a function that can not be calculated without making a decision is the function function (in fact, any function with branches). This is of the form:
 +
<syntaxhighlight lang = "Pascal">
 +
if (operand <0) then (result = -operand) else (result = operand);
 +
</ Syntaxhighlight>
  
−
Cum asupra valorilor numerice pot fi aplicați operatori numerici (adunare, scădere, înmulțire), și asupra valorilor logice, pot fi aplicați operatori logici (ȘI, SAU, NU, SAU EXCLUSIV). Aceștia sunt explicați în detaliu pe pagina Wikipedia a [http://en.wikipedia.org/wiki/Boolean_algebra algebrei booleane].
+
The expression (operand <0) is what is called a logical expression. Logical phrases in [http://en.wikipedia.org/wiki/Boolean_algebra Boolean algebra] can only take two values: '' '' 'true' '' '' or '' '' 'false' '' '. These values ​​can be denoted by the same symbols that we use for numerical values ​​in the second base, ie '' '' '' 0 '' '' 'for false value' '' '' and '' '' '' '' '' 'For truth value' '' '' true (true) '' '' '.
  
−
Concluzia este că folosind aceleași două simboluri, putem face calcule, folosind algebra binară, dar putem exercita control asupra unei funcții, folosind algebra booleană. După cum simbolurile se suprapun pentru computație și control, și operatorii asociați pot avea aceeași formă, și atunci distincția se face doar prin interpretarea lor. Spre exemplu, tabelul cu rezultate pentru înmulțirea a două numere de un bit (operație numerică) arată în felul următor:
+
How numeric operators can be applied to numerical operators (addition, subtraction, multiplication) and logical values ​​can be applied to logical operators (AND, OR, NOT, OR EXCLUSIVELY). These are explained in detail on the Wikipedia page of the [http://en.wikipedia.org/wiki/Boolean_algebra boolean algebra].
  
−
{| class="wikitable"
+
The conclusion is that using the same two symbols, we can do calculations using binary algebra, but we can exercise control over a function using boolean algebra. As the symbols overlap for computation and control, the associated operators may have the same form, and then the distinction is made only by their interpretation. For example, the result table for multiplying two two-digit numbers (numerical operation) looks like this:
−
|- bgcolor="#ddeeff" align="center"
+
 
−
|colspan=2|'''INTRARE''' || '''IEȘIRE'''
+
{| class = "wikitable"
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 +
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
 +
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A * B
 
| A || B || A * B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 0
+
| 0 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 0
+
| 0 || 1 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 0
+
| 1 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 1
+
| 1 || 1 || 1
 
|}
 
|}
  
−
În același timp, operația logică ȘI care întoarce 1 dacă și numai dacă ambii operanzi sunt 1 (mă duc la film DACĂ nu plouă ȘI am bani), are următorul tabel de adevăr:
+
At the same time, the logical AND operation which returns 1 if and only if both operands are 1 (I go to film IF it does not rain AND I have money), has the following table of truth:
  
−
{| class="wikitable"
+
{| class = "wikitable"
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INTRARE''' || '''IEȘIRE'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
| A || B || A ȘI B
+
| A || B || A AND B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 0
+
| 0 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 0
+
| 0 || 1 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 0
+
| 1 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 1
+
| 1 || 1 || 1
 
|}
 
|}
  
−
Se observă că cele două funcții sunt identice. În acest fel, distincția dintre valoare logică și valoare numerică (respectiv operator logic și operator numeric) ține de interpretarea valorilor de intrare (dacă acestea sunt valori logice sau numerice) iar implementarea operatorilor este identică (prin urmare circuitul asociat este identic).
+
It is noted that the two functions are identical. In this way, the distinction between logical value and numerical value (logical operator and numeric operator) is the interpretation of the input values ​​(if these are logical or numerical values) and the implementation of the operators is identical (therefore the associated circuit is identical).
  
 
=== Circuits ===
 
=== Circuits ===
  
−
[[Fișier:Not_gate.png|thumb|Symbol for inverter(A - input, out - output)]]
+
[[File: Not_gate.png | thumb | Invert symbol (A - input, out - out)]]
−
[[Fișier:CMOS_inverter.png|thumb|Inverter built by CMOS transistors]]
+
[[File: CMOS_inverter.png | thumb | Inverter composed of CMOS transistors]]
  
−
In digital electronics, as in whole the digital circuit technology (computers) as in IT, an element that can have a binary value associated to a binary symbol is called [http://en.wikipedia.org/wiki/Bit bit]. The basis of the digital circuits, however complex they may be, is given by its sub-circuits that compute unary and binary operations (one or two operands) using two bits. Such a circuit is called gate (en:[http://en.wikipedia.org/wiki/Logic_gate gate]). The same gate may be considered as an implementation of a bit operator (but also as a logic operator)
+
In digital electronics, as a matter of fact in the whole branch of digital circuitry (ie computers) technology as well as in the information terrain, an element that can take a binary value associated with a binary symbol is called [http: //en.wikipedia. org / wiki / Bit bit]. The basis of digital circuits, however complex, is given by the sub-circuits that compute the single and binary operations (i.e., which have one or two operands) between two bits. Such a sub-circuit is called gate (en: [http://en.wikipedia.org/wiki/Logic_gate gate]). The same gateway can be considered the implementation of a one-bit numeric operator, but also the implementation of a logical operator.
  
−
The way of coding the values associated to binary symbols, in digital electronics, is by a difference in potential between two points. In current technology ([http://en.wikipedia.org/wiki/CMOS CMOS]), a voltage between 0 and about Vdd/2 is associated to a binary value of 0 and a voltage between about Vdd/2 and Vdd, to a value of 1. [http://en.wikipedia.org/wiki/Logic_level]
+
The way to encode the values ​​associated with binary symbols in digital electronics is through a potential difference between two points. In the current technology used ([http://en.wikipedia.org/wiki/CMOS CMOS]), a voltage between 0 and Vdd / 2 is associated with the binary value of 0 and a voltage between Vdd / 2 and Vdd of the binary value of 1 . [http://en.wikipedia.org/wiki/Logic_level]
  
−
One of the simplest gates is the one that implements the logical negation (has only one single input and one output that is always different than the input; that is, for the 0 input, the output is 1 and for the 1 input, the output is 0). This gate is called inverter, or NOT gate (en: [http://en.wikipedia.org/wiki/Inverter_(logic_gate) inverter], NOT gate).
+
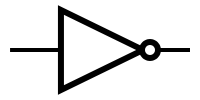
The simplest gate is the one that implements the denial logic operation (it has a single input and a single output that is always different from the input, ie for input 0, output is 1 and for input 1, the output is 0). This gate is called inverse, or bears NO (NOT: http://en.wikipedia.org/wiki/Inverter_(logic_gate) inverter, NOT gate).
  
−
The symbols and the truth tables for the most used gates:
+
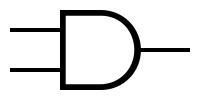
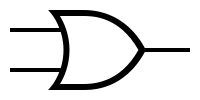
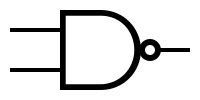
Symbols and truth tables for the most-used gates:
  
−
{| class="wikitable"
+
{| class = "wikitable"
−
! Type !! Symbol !! Truth table !! Type !! Symbol !! Truth table
+
! Tip !! Symbol !! Table of truth !! Tip !! Symbol !! Table of truth
−
|-
+
| -
−
| '''AND'''
+
| '' 'And' ''
−
| [[Image:and.png|AND symbol]]
+
| [[Image: and.png | AND symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INPUT''' || '''OUTPUT'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A AND B
 
| A || B || A AND B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 0
+
| 0 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 0
+
| 0 || 1 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 0
+
| 1 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 1
+
| 1 || 1 || 1
 
|}
 
|}
−
| '''OR'''
+
| '' 'OR' ''
−
| [[Image:or.png|OR symbol]]
+
| [[Image: or.png | OR symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INPUT''' || '''OUTPUT'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A OR B
 
| A || B || A OR B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 0
+
| 0 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 1
+
| 0 || 1 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 1
+
| 1 || 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 1
+
| 1 || 1 || 1
 
|}
 
|}
−
|-
+
| -
−
| '''NOT'''
+
| '' 'NOT' ''
−
| [[Image:not.png|NOT symbol]]
+
| [[Image: not.png | NOT symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|'''INTRARE''' || '''IEȘIRE'''
+
| '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || NOT A
 
| A || NOT A
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1
+
| 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0
+
| 1 || 0
 
|}
 
|}
−
| '''NAND'''
+
| '' 'NAND' ''
−
| [[Image:nand.png|NAND symbol]]
+
| [[Image: nand.png | NAND symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INPUT''' || '''OUTPUT'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A NAND B
 
| A || B || A NAND B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 1
+
| 0 || 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 1
+
| 0 || 1 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 1
+
| 1 || 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 0
+
| 1 || 1 || 0
 
|}
 
|}
−
|-
+
| -
−
| '''NOR'''
+
| '''CLOUD'''
−
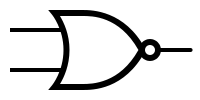
| [[Image:nor.png|NOR symbol]]
+
| [[Image: nor.png | NOR symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INPUT''' || '''OUTPUT'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A NOR B
 
| A || B || A NOR B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 1
+
| 0 || 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 0
+
| 0 || 1 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 0
+
| 1 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 0
+
| 1 || 1 || 0
 
|}
 
|}
−
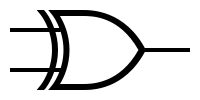
| '''XOR'''
+
| '' 'XOR' ''
−
| [[Image:xor.png|XOR symbol]]
+
| [[Image: xor.png | XOR symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INPUT''' || '''OUTPUT'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A XOR B
 
| A || B || A XOR B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 0
+
| 0 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 1
+
| 0 || 1 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 1
+
| 1 || 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 0
+
| 1 || 1 || 0
 
|}
 
|}
−
|-
+
| -
−
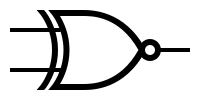
| '''XNOR'''
+
| '' 'XNOR' ''
−
| [[Image:xnor.png|XNOR symbol]]
+
| [[Image: xnor.png | XNOR symbol]]
 
|
 
|
−
{| class="wikitable" align=right
+
{| class = "wikitable" align = right
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
−
|colspan=2|'''INPUT''' || '''OUTPUT'''
+
| colspan = 2 | '' 'INTRARE' '' || '' 'EXIT' ''
−
|- bgcolor="#ddeeff" align="center"
+
| - bgcolor = "# ddeeff" align = "center"
 
| A || B || A XNOR B
 
| A || B || A XNOR B
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 0 || 1
+
| 0 || 0 || 1
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|0 || 1 || 0
+
| 0 || 1 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 0 || 0
+
| 1 || 0 || 0
−
|- bgcolor="#ddffdd" align="center"
+
| - bgcolor = "# ddffdd" align = "center"
−
|1 || 1 || 1
+
| 1 || 1 || 1
 
|}
 
|}
 
|}
 
|}
  
−
As in symbolic representation of the operational amplifiers, the gates also do not have the power lines drawn (Vdd and Vss), as they are visible in CMOS inverter. These are implicitly connected to the powerlines.
+
As with the symbolic representation of the operational amplifiers, it is noticed that neither the logic gates were represented by the power ports (Vdd and Vss), visible on the CMOS inverter schema. They are implicitly connected to the power supply, respectively to the mains.
  
 
== Verilog HDL ==
 
== Verilog HDL ==
  
−
Nowadays, a digital circuit can have in excess of 10 billion gates. This implies the need for the tools allowing design process automation. This, can be done by using hardware description languages ([http://en.wikipedia.org/wiki/Hardware_description_language Hardware Description Languages]).
+
At present, a digital circuit can reach up to 1 billion gates. This implies that we need tools to automate the design process. This can be done using hardware description languages ​​([http://en.wikipedia.org/wiki/Hardware_description_language Hardware Description Languages]). These languages ​​are specially designed to describe a digital circuit, either in terms of behavior or in terms of structure. Clearly, a behavioral description of a circuit will be more succinct, but will not provide information about the desired structure (gate-level), while a structural description will be more accurate in terms of circuit components, but more long and perhaps more difficult to understand.
−
 
 
−
These languages are specifically build for describing a digital circuit either from behavioural point-of-view or from the structural pov. Obviously
 
−
 
 
−
, but will not offer info about the desired structure (gate-level), while a more detailed structured will be more exact
 
−
 
 
−
These languages ​​are specially designed to describe a digital circuit, either in terms of behavior or in terms of structure. Clearly, a behavioral description of a circuit will be more succinct, but will not provide information about the desired structure (gate-level), while a structural description will be more accurate in terms of circuit components, but more long and perhaps more difficult to understand.
 
  
−
There are two very popular hardware description languages: [http://en.wikipedia.org/wiki/Verilog Verilog] and [http://en.wikipedia.org/wiki/VHDL VHDL]. In the continuation of this Digital Integrated Circuits, we will use the Verilog language for circuit descriptions. Its syntax is simple and is partly inherited from C. However, it is very important to note that Verilog is not a programming language. It does not "run" sequentially by a processor, it synthesizes in a circuit or simulates it. Therefore, Verilog users need to decipher to think sequentially as if each line of code is running after the previous one, and rather they have to imagine how the circuit that that code describes. Thus, the most interesting difference with a programming language is that the order of the code blocks in a module does not matter.
+
There are two very popular hardware description languages: [http://en.wikipedia.org/wiki/Verilog Verilog] and [http://en.wikipedia.org/wiki/VHDL VHDL]. In the continuation of this Digital Integrated Circuits Lab, we will use the Verilog language for circuit descriptions. Its syntax is simple and is partly inherited from C. However, it is very important to note that Verilog is not a programming language. It does not "run" sequentially by a processor, it synthesizes in a circuit or simulates it. Therefore, Verilog users need to decipher to think sequentially as if each line of code is running after the previous one, and rather they have to imagine how the circuit that that code describes. Thus, the most interesting difference with a programming language is that the order of the code blocks in a module does not matter.
  
−
Before you start working with some simulation and synthesis software, go through the tutorial explaining the [[Verilog]] syntax.
+
Before you start working with some simulation and synthesis software, go through the tutorial explaining the syntax [[Verilog]

Versiunea de la data 11 aprilie 2018 20:41

Introduction to Digital Circuits

Analog Sign

Analog Signals

Starting with electro-kinetics lessons from high school physics classes (voltage sources, resistors, capacitors, coils, etc.) and ending with Electronic Devices and Circuits, the studied systems were made up of analogue circuit components . Analog circuits are circuits in which the studied quantities (current, voltage) vary continuously at certain intervals. A concrete example is an audio amplifier that picks up an analog audio signal and amplifies it to be transmitted further to a speaker system. You can see an example of an analog signal in the figure below. Of course, this image is generated by a computer, which is a digital device, so it can not represent a true analog signal but can only simulate such a signal with some precision.

Digital Signals

Sample signal (discreet in time with continuous values)
Quantized signal (continuous time with discrete values)
Digital signal (quantized and sampled)

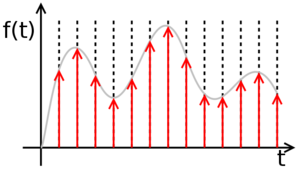
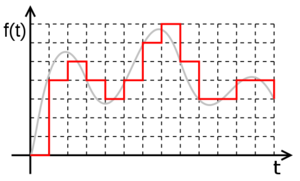
A digital signal is a set of discrete values, each of these values ​​being part of a discrete set of rational values. Transforming an analog signal into a digital signal implies a loss of precision. Let's take for example a simple sinusoidal analog signal, representing the time variation of the voltage at the terminals of a resistor. Between the moments t = 0 and t = 1, the function, being continuous, has an infinity of values, so it is impossible to isolate each value, the sequence thus obtained being infinite. The procedure, in this situation, is to isolate only some of the values, at certain times, called samples, so that we get a finite set of values. This procedure is called sampling and the time period between two successive samples is called the sampling period. The shorter the sampling period (or the higher sampling frequency), the better the digital signal is a more accurate copy (lower precision loss) than the original analog signal. If, however, the analog signal is limited bandwidth (ie it can be written as a finite sum of sinusoidal signals), then sampling theorem shows that if the sampling is done at a frequency at least twice as high as the maximum frequency of the signal spectrum, of the sample series can be obtained with 100% accuracy of the original analog signal.


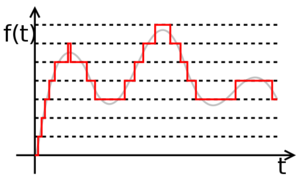
However, there is still a problem. The signal being continuous, the sample values ​​are in a continuous space, therefore of infinite precision. To reduce the accuracy of values, use a method called quantization. This process involves dividing the range of possible signal values ​​into subdivisions. The more subtle these subdivisions, the higher the values ​​obtained by the quantization will be closer to the real values ​​of the original signal, but will be represented by a more number of symbols.


In conclusion, a digital signal is a sequence of numbers obtained by sampling and quantization of an analog signal.

Numbers and symbols. Numbering Bases

As noted in the previous chapter, a digital signal is a string of values. These values ​​are represented by symbols, belonging to a numbering base. The simplest example is the one we are all accustomed to, that is, the decimal point, using the figures from 0 to 9 as symbols. But this is by no means the only one. Other examples would be the Roman numeration system where symbols I, V, X, L, C, D, and M are used as symbols, where the value of these symbols in a number depends on their order. The same can be said about the decimal numbering base where, for example, the symbol 9 has another value if it is in the first position (9) than if it is on the second (90). What is interesting to note is that, despite the mental association between the symbols we have been used to working with and the numerical values ​​they express, the two notions are completely distinct. The value "ten" can be expressed numerically in the decimal number as 10 in the Roman numeration system as X in the hexadecimal system as A in the binary system as 1010 in the octal as 12 but all these representations actually express the same number.

Binary numbering system

As the name says, this system uses only two symbols, most of them being 0 and 1. Therefore, a number can be represented in the binary system (also called base 2) as a sequence of 0 and 1 The order of the symbols in a written number in the second base follows the same rules as the numbers written in the decimal. Thus, if in a decimal number, the number 7 in position 4 was equivalent to 7 * 10 4 </ sup>, where 10 is equal to the number of distinct symbols used, then to base 2, 4 is equivalent to 1 * 2 4 </ sup>. This is also the rule for converting the numbers from base 2 to base 10. Therefore:

1001010 (2) </ sub> = 1 * 2 6 </ sup> + 0 * 2 3 </ sup> + 0 * 2 2 </ sup> 0 + 8 + 0 + 2 + 0 = 54 (10) </ sub>

Transforming a number from the decimal to the binary involves the repeated division into 2 (the number of base symbols), where the split at each iteration is given by the previous division. The operation is repeated as long as it is different than 0. The binary number is given by the remainder sequence from the last division to the first.

The advantage of the binary system is that the reduced number of symbols makes the number of possible operations between two random symbols reduced, so it is easy to imagine a physical realization of some circuits to implement these operations. The disadvantage is that for relatively small numbers, many symbols are needed for representation. Therefore, for the flexibility of the operation with values ​​represented by many symbols, the hexadecimal numbering base is used, ie the base 16. As the name says, the hexadecimal base uses 16 symbols: the digits 0 to 9, and the characters a, b, c d, e and f. The use of base 16 is advantageous due to the very slight passage between it and base 2. Thus, at any value represented by a sequence of four binary symbols, one and only one hexadecimal symbol corresponds.

Computation and control

We have therefore come to the conclusion that calculations can be made using only two symbols corresponding to zero and one. We have a numbering base (base two) that can be used to make the most complex calculations with the same accuracy as the decimal ones. But besides the actual calculation, a computer system must be able to make decisions, that is to say, to evaluate an expression and decide its value of truth, a general type of operation 'if' else . The simplest example of a function that can not be calculated without making a decision is the function function (in fact, any function with branches). This is of the form: <syntaxhighlight lang = "Pascal"> if (operand <0) then (result = -operand) else (result = operand); </ Syntaxhighlight>

The expression (operand <0) is what is called a logical expression. Logical phrases in Boolean algebra can only take two values: 'true' or 'false' '. These values ​​can be denoted by the same symbols that we use for numerical values ​​in the second base, ie 0 'for false value' and 'For truth value' true (true) '.

How numeric operators can be applied to numerical operators (addition, subtraction, multiplication) and logical values ​​can be applied to logical operators (AND, OR, NOT, OR EXCLUSIVELY). These are explained in detail on the Wikipedia page of the boolean algebra.

The conclusion is that using the same two symbols, we can do calculations using binary algebra, but we can exercise control over a function using boolean algebra. As the symbols overlap for computation and control, the associated operators may have the same form, and then the distinction is made only by their interpretation. For example, the result table for multiplying two two-digit numbers (numerical operation) looks like this:

- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A * B - bgcolor = "# ddffdd" align = "center" 0 0 0 - bgcolor = "# ddffdd" align = "center" 0 1 0 - bgcolor = "# ddffdd" align = "center" 1 0 0 - bgcolor = "# ddffdd" align = "center" 1 1 1

At the same time, the logical AND operation which returns 1 if and only if both operands are 1 (I go to film IF it does not rain AND I have money), has the following table of truth:

- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A AND B - bgcolor = "# ddffdd" align = "center" 0 0 0 - bgcolor = "# ddffdd" align = "center" 0 1 0 - bgcolor = "# ddffdd" align = "center" 1 0 0 - bgcolor = "# ddffdd" align = "center" 1 1 1

It is noted that the two functions are identical. In this way, the distinction between logical value and numerical value (logical operator and numeric operator) is the interpretation of the input values ​​(if these are logical or numerical values) and the implementation of the operators is identical (therefore the associated circuit is identical).

Circuits

Invert symbol (A - input, out - out)
Inverter composed of CMOS transistors

In digital electronics, as a matter of fact in the whole branch of digital circuitry (ie computers) technology as well as in the information terrain, an element that can take a binary value associated with a binary symbol is called [http: //en.wikipedia. org / wiki / Bit bit]. The basis of digital circuits, however complex, is given by the sub-circuits that compute the single and binary operations (i.e., which have one or two operands) between two bits. Such a sub-circuit is called gate (en: gate). The same gateway can be considered the implementation of a one-bit numeric operator, but also the implementation of a logical operator.

The way to encode the values ​​associated with binary symbols in digital electronics is through a potential difference between two points. In the current technology used (CMOS), a voltage between 0 and Vdd / 2 is associated with the binary value of 0 and a voltage between Vdd / 2 and Vdd of the binary value of 1 . [1]

The simplest gate is the one that implements the denial logic operation (it has a single input and a single output that is always different from the input, ie for input 0, output is 1 and for input 1, the output is 0). This gate is called inverse, or bears NO (NOT: http://en.wikipedia.org/wiki/Inverter_(logic_gate) inverter, NOT gate).

Symbols and truth tables for the most-used gates:

Tip Symbol Table of truth Tip Symbol Table of truth - 'And' AND symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A AND B - bgcolor = "# ddffdd" align = "center" 0 0 0 - bgcolor = "# ddffdd" align = "center" 0 1 0 - bgcolor = "# ddffdd" align = "center" 1 0 0 - bgcolor = "# ddffdd" align = "center" 1 1 1
'OR' OR symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A OR B - bgcolor = "# ddffdd" align = "center" 0 0 0 - bgcolor = "# ddffdd" align = "center" 0 1 1 - bgcolor = "# ddffdd" align = "center" 1 0 1 - bgcolor = "# ddffdd" align = "center" 1 1 1
- 'NOT' NOT symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A NOT A - bgcolor = "# ddffdd" align = "center" 0 1 - bgcolor = "# ddffdd" align = "center" 1 0
'NAND' NAND symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A NAND B - bgcolor = "# ddffdd" align = "center" 0 0 1 - bgcolor = "# ddffdd" align = "center" 0 1 1 - bgcolor = "# ddffdd" align = "center" 1 0 1 - bgcolor = "# ddffdd" align = "center" 1 1 0
- CLOUD NOR symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A NOR B - bgcolor = "# ddffdd" align = "center" 0 0 1 - bgcolor = "# ddffdd" align = "center" 0 1 0 - bgcolor = "# ddffdd" align = "center" 1 0 0 - bgcolor = "# ddffdd" align = "center" 1 1 0
'XOR' XOR symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A XOR B - bgcolor = "# ddffdd" align = "center" 0 0 0 - bgcolor = "# ddffdd" align = "center" 0 1 1 - bgcolor = "# ddffdd" align = "center" 1 0 1 - bgcolor = "# ddffdd" align = "center" 1 1 0
- 'XNOR' XNOR symbol
- bgcolor = "# ddeeff" align = "center" 'INTRARE' 'EXIT' - bgcolor = "# ddeeff" align = "center" A B A XNOR B - bgcolor = "# ddffdd" align = "center" 0 0 1 - bgcolor = "# ddffdd" align = "center" 0 1 0 - bgcolor = "# ddffdd" align = "center" 1 0 0 - bgcolor = "# ddffdd" align = "center" 1 1 1

As with the symbolic representation of the operational amplifiers, it is noticed that neither the logic gates were represented by the power ports (Vdd and Vss), visible on the CMOS inverter schema. They are implicitly connected to the power supply, respectively to the mains.

Verilog HDL

At present, a digital circuit can reach up to 1 billion gates. This implies that we need tools to automate the design process. This can be done using hardware description languages ​​(Hardware Description Languages). These languages ​​are specially designed to describe a digital circuit, either in terms of behavior or in terms of structure. Clearly, a behavioral description of a circuit will be more succinct, but will not provide information about the desired structure (gate-level), while a structural description will be more accurate in terms of circuit components, but more long and perhaps more difficult to understand.

There are two very popular hardware description languages: Verilog and VHDL. In the continuation of this Digital Integrated Circuits Lab, we will use the Verilog language for circuit descriptions. Its syntax is simple and is partly inherited from C. However, it is very important to note that Verilog is not a programming language. It does not "run" sequentially by a processor, it synthesizes in a circuit or simulates it. Therefore, Verilog users need to decipher to think sequentially as if each line of code is running after the previous one, and rather they have to imagine how the circuit that that code describes. Thus, the most interesting difference with a programming language is that the order of the code blocks in a module does not matter.

Before you start working with some simulation and synthesis software, go through the tutorial explaining the syntax [[Verilog]

Adus de la „http://wiki.dcae.pub.ro/index.php?title=Introduction._Verilog_HDL_(Verilog_syntax)&oldid=5788”