Diferență între revizuiri ale paginii „ROM Memory”
Cbira (discuție | contribuții) (Pagină nouă: Most functions implemented by combinational circuits can be described analytically, ie the output can be calculated by applying operators (addition, subtraction, shift, logic o...) |
Cbira (discuție | contribuții) |
||
| Linia 5: | Linia 5: | ||
[[File: rom0.png | thumb | ROM interface]] | [[File: rom0.png | thumb | ROM interface]] | ||
| − | A ROM, as a circuit, has a single input, which specifies the input value, and a single output on which the function value for the specified input propagates. For each entry value, a ROM has a memory location that is accessed when the corresponding value appears on the input port. The location value is propagated to the output port. Thus, a ROM has''' two important parameters | + | A ROM, as a circuit, has a single input, which specifies the input value, and a single output on which the function value for the specified input propagates. For each entry value, a ROM has a memory location that is accessed when the corresponding value appears on the input port. The location value is propagated to the output port. Thus, a ROM has''' two important parameters: |
#the bit number of the input port (representing the memory address), which determines the total number of memory locations, denoted M; | #the bit number of the input port (representing the memory address), which determines the total number of memory locations, denoted M; | ||
#bit number of the output port (equal to the number of bits of each memory location), denoted N; | #bit number of the output port (equal to the number of bits of each memory location), denoted N; | ||
| − | '''Note:''' If the input port has M bits, then the total number of possible addresses or the total number of ROM locations is '''2 <sup> M </sup>'''. So the total number of ROMs (memory capacity) is the product of the total number of locations ('''2 <sup> M </sup>' ') and the bit size of a location ('''). | + | '''Note:''' If the input port has M bits, then the total number of possible addresses or the total number of ROM locations is '''2 <sup> M </sup>'''. So the total number of ROMs (memory capacity) is the product of the total number of locations ('''2 <sup> M </sup>''') and the bit size of a location ('''). |
[[File: rom1.png | ROM example (diagram)]] | [[File: rom1.png | ROM example (diagram)]] | ||
Versiunea de la data 12 aprilie 2018 07:53
Most functions implemented by combinational circuits can be described analytically, ie the output can be calculated by applying operators (addition, subtraction, shift, logic operations) of the inputs. Such functions are those that you have implemented in lab 1 and 2. However, there are cases where there is no clear relationship between the input value and the output value, so a rule can not be applied for calculating the latter. In this case, the solution is to use a Read-Only Memory (ROM), also called the Lookup Table (LUT), which has the role of storing the corresponding output value for each input value.
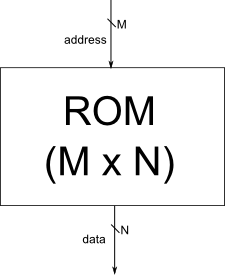
Interface of ROM ROM
A ROM, as a circuit, has a single input, which specifies the input value, and a single output on which the function value for the specified input propagates. For each entry value, a ROM has a memory location that is accessed when the corresponding value appears on the input port. The location value is propagated to the output port. Thus, a ROM has two important parameters:
- the bit number of the input port (representing the memory address), which determines the total number of memory locations, denoted M;
- bit number of the output port (equal to the number of bits of each memory location), denoted N;
Note: If the input port has M bits, then the total number of possible addresses or the total number of ROM locations is 2 M . So the total number of ROMs (memory capacity) is the product of the total number of locations (2 M ) and the bit size of a location ().
Implementing a ROM memory
Being a combined circuit in Verilog, deploying a ROM can be done in three ways:
- with blocks assign and conditional operator;
- with blocks always combinational and sub-blocks if;
- with always blocks' and 'blocks''' blocks.
The preferred method is the last because of the ease of the description (see Conditional Operators).