Diferență între revizuiri ale paginii „CID Aplicatii 9”
| Linia 37: | Linia 37: | ||
initial begin | initial begin | ||
clock_t = 0; | clock_t = 0; | ||
| − | forever #1 clock_t = clock_t | + | forever #1 clock_t = ~clock_t; |
end | end | ||
| Linia 88: | Linia 88: | ||
.clock(clock), | .clock(clock), | ||
.reset(reset), | .reset(reset), | ||
| − | + | .count(count) | |
); | ); | ||
| Linia 109: | Linia 109: | ||
initial begin | initial begin | ||
clock_t = 0; | clock_t = 0; | ||
| − | forever #1 clock_t = clock_t | + | forever #1 clock_t = ~clock_t; |
end | end | ||
| Linia 144: | Linia 144: | ||
always @(posedge clk) cnt <= cnt + 1; | always @(posedge clk) cnt <= cnt + 1; | ||
| + | |||
| + | //urmatorul bloc initial este folosit exclusiv de catre simulare (va fi ignorat de sinteza) | ||
| + | //si ne permite initializarea numaratorului in simulare atunci cand nu avem reset | ||
| + | initial begin | ||
| + | cnt = 0; | ||
| + | end | ||
| + | // | ||
endmodule | endmodule | ||
Versiunea curentă din 26 aprilie 2021 15:20
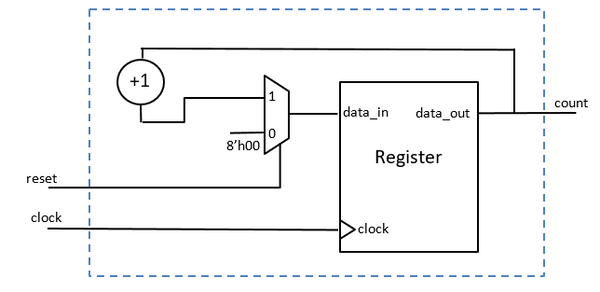
1. Numaratorul
Numaratorul este cel mai simplu automat, fiind format dintr-un registru ce retine valoarea curenta a acestuia si un circuit de incrementare ce genereaza la iesirea sa valoarea ce va trebui stocata in registru la urmatorul front crescator de ceas (valoarea curenta incrementata cu 1). In figura de mai jos este reprezentat un numarator cu reset sincron:
Implementarea Numaratorului cu reset sincron
module Numarator
#(parameter WIDTH = 8)
(
input clock,
input reset,
output reg [WIDTH-1:0] count
);
always@(posedge clock) begin
if(reset == 0)
count <= 0;
else
count <= count + 1;
end
endmodule
Implemenatarea unui modul de test pentru numarator
`timescale 1ns/1ps
module Numarator_TB();
parameter WIDTH_T = 5;
reg reset_t, clock_t;
wire [WIDTH_T-1:0] count_t;
initial begin
clock_t = 0;
forever #1 clock_t = ~clock_t;
end
initial begin
reset_t = 0;
#2 reset_t = 1;
#500 $stop();
end
Numarator #(.WIDTH(WIDTH_T)) DUT(
.clock(clock_t),
.reset(reset_t),
.count(count_t)
);
endmodule
Observatie: Cat timp semnalul reset este inactiv, numaratorul isi va incrementa valoarea la fiecare front crescator de ceas. Cand va ajunge la valoarea sa maxima (de exemplu, 31), va avea loc o depasire, dar avand la dispozitie un numar limitat de biti (de exemplu, 5), semnalul de iesire va avea valoarea 0 (retinem doar cei mai putin semnificativi 5 biti), circuitul pornind din nou numaratoarea.
2. Divizorul de frecventa cu factor de divizare putere a lui 2
Daca urmarim figura de mai jos in care sunt reprezentate variatiile fiecarui bit in timpul functionarii unui numarator pe 4 biti, observam ca, cu cat ordinul bitului creste (este mai semnificativ), frecventa de variatie este mai mica. Intre frecventele de variatie corespunzatoare a doi biti succesivi exista urmatoarea relatie: frecventa unui bit este de doua ori mai mica decat frecventa bitului anterior (mai putin semnificativ).
Observand ca frecventa bitului 0 este de doua ori mai mica decat cea a ceasului, putem concluziona ca frecventa de variatie a bitului cu indicele N este data de: fbN = fclk / 2N+1
Asadar, pentru a crea un divizor de frecventa cu factor de divizare putere a lui 2, putem folosi un numarator indeajuns de mare, din care extragem bitul cu frecventa dorita.
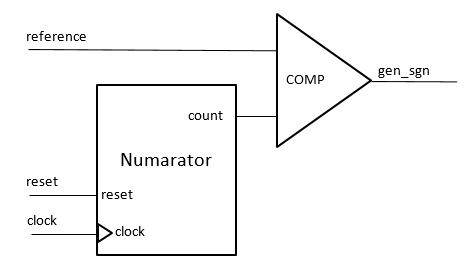
3. Generator de semnal cu factor de umplere variabil
Pentru a genera un semnal cu factor de umplere variabil, putem folosi un numarator si un comparator. Frecventa semnalului va ramane mereu aceeasi si va fi data de dimensiunea numaratorului (o perioada este egala cu timpul necesar pentru ca numaratorul sa faca un ciclu complet 0 - maxim). Singurul lucru care se modifica aici este factorul de umplere: raportul dintre cat sta in 1 un semnal de-a lungul unei perioade si cat sta in 0.
'Implementarea circuitului de generare a unui semnal cu factor de umplere variabil
module Generator
#( parameter WIDTH = 8)
(
input [WIDTH-1:0] reference,
input clock,
input reset,
output gen_sgn
);
wire [WIDTH-1:0] count;
Numarator #(.WIDTH(WIDTH)) Counter (
.clock(clock),
.reset(reset),
.count(count)
);
assign gen_sgn = (count < reference) ? 1:0;
endmodule
Implementarea modulului de test
`timescale 1ns/1ps
module Generator_TB();
parameter WIDTH_T = 5;
reg reset_t, clock_t;
reg [WIDTH_T-1:0] reference_t;
wire gen_sgn_t;
initial begin
clock_t = 0;
forever #1 clock_t = ~clock_t;
end
initial begin
reset_t = 0;
reference_t = 10;
#2 reset_t = 1;
#500 $stop();
end
Generator #(.WIDTH(WIDTH_T)) DUT(
.clock(clock_t),
.reset(reset_t),
.reference(reference_t),
.gen_sgn(gen_sgn_t)
);
endmodule
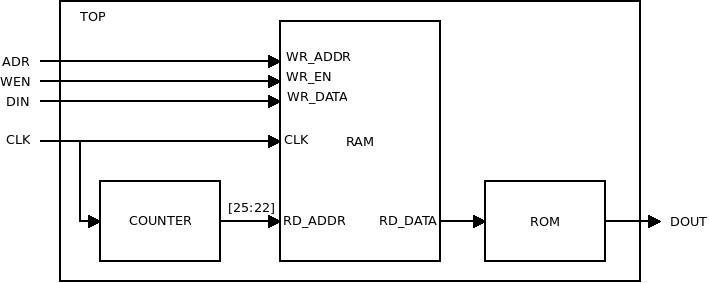
4. Exercitiu
Implementati circuitul descris prin schema de mai jos, stiind ca RAM este o memorie 16x4b, cu citire sincrona:
Implementarea modulului COUNTER
module COUNTER(
input clk,
output reg [31:0] cnt
);
always @(posedge clk) cnt <= cnt + 1;
//urmatorul bloc initial este folosit exclusiv de catre simulare (va fi ignorat de sinteza)
//si ne permite initializarea numaratorului in simulare atunci cand nu avem reset
initial begin
cnt = 0;
end
//
endmodule
Implementarea modulului ROM
module ROM(
input [3:0] in,
output reg [3:0] out
);
always @(in)
case(in)
0: out = 4'b0000;
1: out = 4'b0110;
2: out = 4'b0011;
3: out = 4'b1110;
4: out = 4'b1011;
5: out = 4'b1111;
6: out = 4'b0111;
7: out = 4'b1100;
8: out = 4'b0001;
9: out = 4'b0101;
10: out = 4'b1101;
11: out = 4'b1010;
12: out = 4'b0010;
13: out = 4'b0100;
14: out = 4'b1000;
15: out = 4'b1001;
default: out = 4'b0000;
endcase
endmodule
Implementarea modulului RAM
module RAM(
input clk,
input wr_en,
input [3:0] rd_addr,
input [3:0] wr_addr,
input [3:0] wr_data,
output reg [3:0] rd_data
);
reg [3:0] memory [0:15];
always@(posedge clk) begin
if(wr_en)
memory[wr_addr] <= wr_data;
rd_data <= memory[rd_addr];
end
endmodule
Implementarea modulului TOP
module TOP(
input [3:0] adr,
input wen,
input [3:0] din,
input clk,
output [3:0] dout
);
wire [31:0] cnt_w;
wire [3:0] data_w;
COUNTER COUNT(
.clk(clk),
.cnt(cnt_w)
);
RAM RAM_MEM(
.clk(clk),
.wr_en(wen),
.rd_addr(cnt_w[25:22]),
.wr_addr(adr),
.wr_data(din),
.rd_data(data_w)
);
ROM ROM_MEM(
.in(data_w),
.out(dout)
);
endmodule