Applications 9

Almost always the FSM is described behaviorally, leaving the CLC gate level generation and optimization to compiler/synthesizer. However, the usual behavioral description closely follows the block structure of the FSM, with one block that computes the transition function and another block that computes the output. The FSMs are of two categories:

• Moore FSM, whose outputs depend only on the current state
• Mealy FSM, whose outputs depend also on inputs

Most often the Mealy FSM is a delayed Mealy FSM. Its output depends on the previous state and on the input values at transition time.

Exercise 1

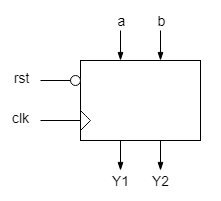
Design an automaton that determines the order in which two buttons are pressed. The buttons generate logic signals, a and b, that are 1 if the corresponding button is pressed. The automaton has two logic outputs, Y1 and Y2. Y1 is asserted if a was pressed first, followed by b. Y2 is asserted if b was pressed first, followed by a. The outputs remain asserted until reset. The reset is active 0.

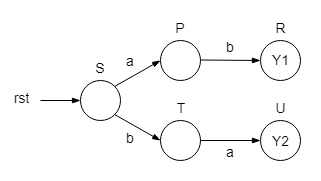
Moore FSM

The circuit may be designed as a Moore FSM, with two separate states for those two particular output configurations. In the graph below only the transitions to different states are shown. If their conditions are not met, the FSM stays in the current state, whatever it is. In the final states, R or U, the automaton stays until reset. From any state the reset forces the FSM to its initial state, S.

State coding

It is not recommended to use explicit values whenever the state variable is used. To make code much more readable and easier to design and debug, the state values are parameters. Another advantage of using parameters is that the state explicit values are declared in a single place, at parameter declaration, therefore if their values need to be changed, only the parameter declaration is affected.

The state values are internal design options, therefore the parameters used for states are local ones. They are declared as local parameters, using the template localparam name=value; The names of parameters are upper case letters, and may include digits and underline.

localparam STATE_S = 3'd0;
localparam STATE_P = 3'd1;
...

Attention!

• The state values must be distinct! Otherwise you may end with a state having multiple names.
• Local parameter declarations are the first statements after the module interface. The order of statements for a module should be the following:

1. module
2. interface declaration (the list of inputs and outputs)
3. localparam declarations
4. internal wire and reg declarations
5. description (structural with instantiations or behavioral with always processes and continuos assignments)
6. endmodule

State transitions

All transitions are grouped in a single sequential always process, with a case statement that groups transitions by current state. The combinational function that computes the next state (the transition function) is implicitly described by the case statement and the statements for each case. The state is updated sequentially because the always process is sensitive only to clock edges.

always @(posedge clk) begin
    if(~rst)
        state <= STATE_S;
    else begin
        case(state)
        STATE_S: begin
            if(a)
                state <= STATE_P;
            else if(b)
                state <= STATE_T;
            else
                state <= state; // stays in the same state
        end
        STATE_P: begin
            if(b)
                state <= STATE_R;
            else
                state <= state;
        end
        // other states with their transitions
        default:
                state <= STATE_S; // from undefined states jump to the initial state
        endcase
    end
end

Attention!

• All assignments inside the sequential process are done with the nonblocking assignment operator, <=
• Don't forget the default case!
• The reg variable for the state must be declared with the required number of bits, which is the same as the number of bits declared for each value of the state value parameters.

Outputs

Since Moore outputs depend only on state they are described either through continuous assignments, or inside a combinational always process.

If continuous assignments are used, the outputs are assigned logic expressions based on state:

assign y1 = (state == R);

The combinational always process is preferred when state values are easier to group by states:

always @(*) begin
    case(state)
    STATE_S: {y1, y2} = 2'b00;
    STATE_P: {y1, y2} = 2'b00;
    STATE_R: {y1, y2} = 2'b10;
    // other states with their outputs
    default: {y1, y2} = 2'b00;
    endcase
end

Attention!

• All assignments inside the combinational process are done with the blocking assignment operator, =
• Don't forget the default case!

Requirements

• Create a new project in a new folder
• Design the automaton as the top level design entity
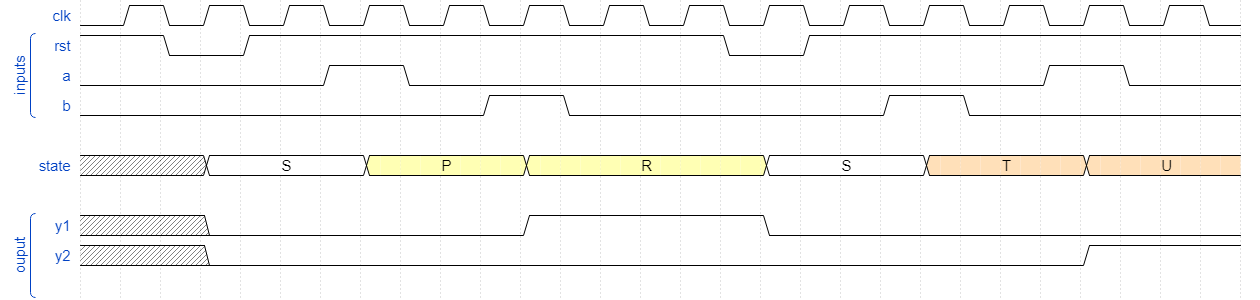
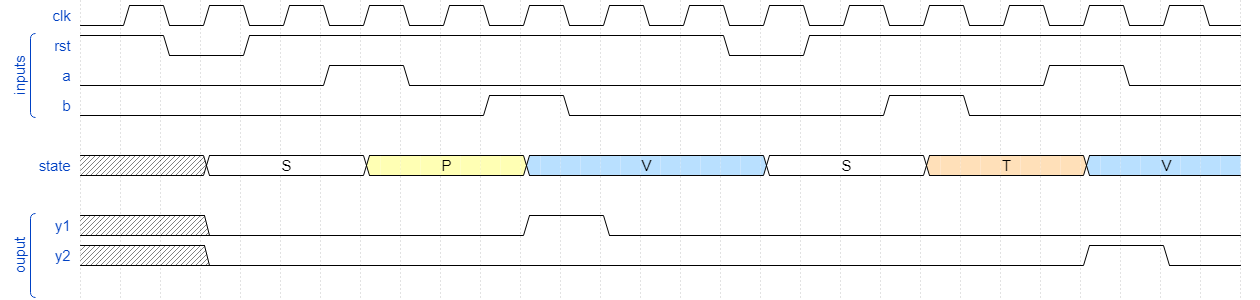
• Design a testbench with the input signals generated as in the figure below.
• Run simulation. If the design is correct the outputs should appear as in the figure.
• To implement the design assign BTN0, BTN1 and BTN2 to rst, a, and b inputs. Assign LED1 and LED2 to y1 and y2 outputs.

Exercise 2

Design an automaton that determines the order in which two buttons are pressed. The buttons generate logic signals, a and b, that are 1 if the corresponding button is pressed. The automaton has two logic outputs, Y1 and Y2. Y1 is asserted if a was pressed first, followed by b. Y2 is asserted if b was pressed first, followed by a. The outputs are asserted for ONLY ONE CLOCK CYCLE. The reset is active 0.

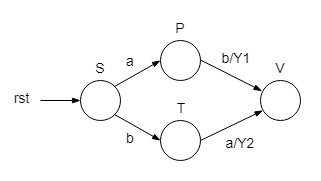
Mealy FSM

The circuit may be designed as a delayed Mealy FSM, with fewer states than if designed as a Moore FSM. In the graph below only the transitions to different states are shown. If their conditions are not met, the FSM stays in the current state, whatever it is. In the final state, V, the outputs are active for one clock cycle, depending on the input values that determined the transition to it. All other transitions are with outputs 0. From any state, the reset forces the FSM to its initial state, S.

State transitions

The transition function is described in the same way as for the Moore FSM. However, there are only 4 states, therefore the state variable and the state value parameters have only 2 bits. The case inside the sequential process for transitions has also fewer cases.

Outputs

Since the delayed Mealy outputs depend both on the previous state AND the previous input values (at the last transition) they are described inside a sequential always process. The outputs must be declared of reg type.

always @(posedge clk) begin
    if(~rst) begin
        y1 <= 1'b0;
        y2 <= 1'b0;
    end
    else begin
        case(state)
        STATE_S: begin
             y1 <= 1'b0;
             y2 <= 1'b0;
        end
        // other states with their outputs
        default: begin
            y1 <= 1'b0;
            y2 <= 1'b0;
        end
        endcase
    end
end

Attention!

• All assignments inside the sequential process are done with the nonblocking assignment operator, <=
• Don't forget the default case!

Requirements

• Use the same project as before
• Redesign the automaton as a Mealy FSM
• The testbench should not be modified.
• Run simulation. If the design is correct the outputs should appear as in the figure below. The differences from the previous waveform are in the state values and output pulses.

Exercise 3

Design an FSM for an automatic chocolate selling machine, which delivers chocolates at 2.5€. The machine accepts only coins of 50 cents and 1 euro, and does not return any change. When the amount of 2.5€ or more is reached, the machine delivers a chocolate and will resume the process, subtracting 2.5€ from the current amount. The process resumes with whatever amount remains after delivering, which may be 0 or 0.5€.

The inputs are the digital signals cents, euro and ack.

When the user inserts a valid coin, the corresponding input, cents or euro, is asserted and stays 1 for some clock cycles. The FSM considers the coin validated only after the corresponding input goes back to 0.

The output is a digital signal, deliver, that is asserted when the amount reaches or surpasses 2.5€ and stays asserted until the input ack is asserted. The FSM resumes the process after ack is deasserted.

The internal states of the FSM may be equivalent to the current amount, 0, 0.5, 1, 1.5, 2, 2.5 and 3 euros.

Implement the FSM for the automatic chocolate selling machine using three push buttons for cents, euro and ack inputs (the pushbutton generates 0 when pressed), an LED to indicate the deliver output, and another pushbutton for the reset (that resets the amount to 0).

Hint

To easy the implementation and keep the FSM as simple as possible, the inputs cents, euro and ack, which are pulses of arbitrary length (that may last hundreds of thousands of clock cycles!), may be transformed to one cycle pulses, asserted during the clock cycle that follows the original pulse. The FSM uses these one clock cycle pulses to compute the transitions.

As an example, the euro input is transformed to euro_p internal signal, whose pulses last one clock cycle. These internal signal is further used by the FSM.

...

reg  euro_d; // delayed version of the euro input
wire euro_p; // one clock cycle pulse to be used by the FSM
...
always @(posedge clk) euro_d <= euro; // euro_d is the copy of euro input, shifted one clock cycle
assign euro_p = euro_d & ~euro; // euro_p is asserted one clock cycle after euro pulse has ended
...