Diferență între revizuiri ale paginii „Introduction. Verilog HDL (Verilog syntax)”
Cbira (discuție | contribuții) |
Cbira (discuție | contribuții) |
||
| Linia 90: | Linia 90: | ||
The way of coding the values associated to binary symbols, in digital electronics, is by a difference in potential between two points. In current technology ([http://en.wikipedia.org/wiki/CMOS CMOS]), a voltage between 0 and about Vdd/2 is associated to a binary value of 0 and a voltage between about Vdd/2 and Vdd, to a value of 1. [http://en.wikipedia.org/wiki/Logic_level] | The way of coding the values associated to binary symbols, in digital electronics, is by a difference in potential between two points. In current technology ([http://en.wikipedia.org/wiki/CMOS CMOS]), a voltage between 0 and about Vdd/2 is associated to a binary value of 0 and a voltage between about Vdd/2 and Vdd, to a value of 1. [http://en.wikipedia.org/wiki/Logic_level] | ||
| − | |||
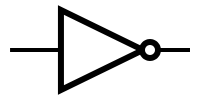
| − | + | One of the simplest gates is the one that implements the logical negation (has only one single input and one output that is always different than the input; that is, for the 0 input, the output is 1 and for the 1 input, the output is 0). This gate is called inverter, or NOT gate (en: [http://en.wikipedia.org/wiki/Inverter_(logic_gate) inverter], NOT gate). | |
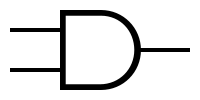
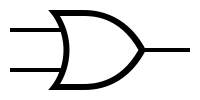
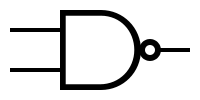
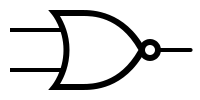
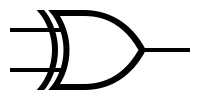
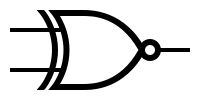
| − | + | The symbols and the truth tables for the most used gates: | |
{| class="wikitable" | {| class="wikitable" | ||
| − | ! | + | ! Type !! Symbol !! Truth table !! Type !! Symbol !! Truth table |
|- | |- | ||
| '''AND''' | | '''AND''' | ||
| Linia 104: | Linia 103: | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| − | |colspan=2|''' | + | |colspan=2|'''INPUT''' || '''OUTPUT''' |
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| A || B || A AND B | | A || B || A AND B | ||
| Linia 121: | Linia 120: | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| − | |colspan=2|''' | + | |colspan=2|'''INPUT''' || '''OUTPUT''' |
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| A || B || A OR B | | A || B || A OR B | ||
| Linia 152: | Linia 151: | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| − | |colspan=2|''' | + | |colspan=2|'''INPUT''' || '''OUTPUT''' |
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| A || B || A NAND B | | A || B || A NAND B | ||
| Linia 170: | Linia 169: | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| − | |colspan=2|''' | + | |colspan=2|'''INPUT''' || '''OUTPUT''' |
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| A || B || A NOR B | | A || B || A NOR B | ||
| Linia 187: | Linia 186: | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| − | |colspan=2|''' | + | |colspan=2|'''INPUT''' || '''OUTPUT''' |
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| A || B || A XOR B | | A || B || A XOR B | ||
| Linia 205: | Linia 204: | ||
{| class="wikitable" align=right | {| class="wikitable" align=right | ||
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| − | |colspan=2|''' | + | |colspan=2|'''INPUT''' || '''OUTPUT''' |
|- bgcolor="#ddeeff" align="center" | |- bgcolor="#ddeeff" align="center" | ||
| A || B || A XNOR B | | A || B || A XNOR B | ||
| Linia 219: | Linia 218: | ||
|} | |} | ||
| − | + | As in symbolic representation of the operational amplifiers, the gates also do not have the power lines drawn (Vdd and Vss), as they are visible in CMOS inverter. These are implicitly connected to the powerlines. | |
== Verilog HDL == | == Verilog HDL == | ||
Versiunea de la data 22 martie 2018 18:43
Introduction to Digital Circuits
Analog signals
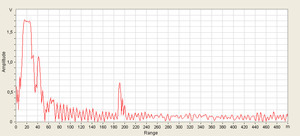
Starting with the classes of electrocinetics of the physics in highschool (power supplies, resistors, capacitors, inductors, etc.) and ending with the classes of Dispozitive și Circuite Electronice, the systems studied were formed by analog components. The analog circuits are circuits where the studied quantity (current, voltage), vary continuously in some intervals. An example would be an audio amplifier which gets the analog sound signal and amplifies it so that it is further sent to the speakers. One may see an example of analog signal in the side figure. Of course, this image generated on a computer (which is a digital device) cannot be represented by a true analog signalm but can only simulates such a signal, with a certain precision.
Digital signals
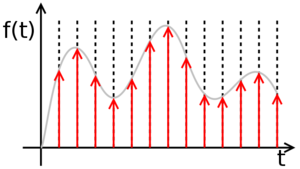
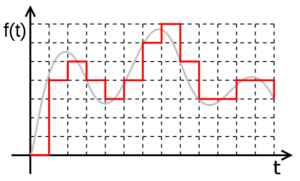
A digital signal is a number of discrete values, each of them being part of a discrete set of rational values. Transforming an analog signal into a digital signal implies a loss of precision. Let's take for example a simple analog sine signal, representing the variation over time, of a voltage across a resistor. At moments t=0 and t=1, the function, being continuous, has an infinity of values, therefore, it is impossible to isolate each value, the resulting series being infinite. The procedure, in this situation, is to isolate just a part of the values, at certain moments in time, called "samples", so that we may get a finite series of values. This procedure is called sampling, anf the time between two consecutive samples is called "sampling period". The shorter the sampling period (higher sampling frequency), the more accurate is the digital signal as a copy of the original analog singal (lower loss of precision). If however the analog signal has limited bandwidth (this means it can be written as a finite sum of sine signals), then, Sampling Theorem proves that if the sampling is performed with a frequency at least double the maxium frequency in the signal's spectrum, from the series of samples one can recover with 100% precision, the original analog signal.
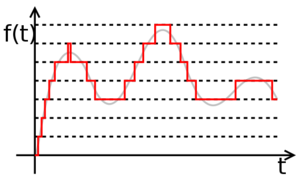
Yet, there is another problem. The continuos signal has samples belonging to a continuous space, therefore of infinite precision. To transform it to discrete, one must reduce the precision of the values; the procedure used is called quantization. This procedure implies splitting the interval of possible values, in a finite number of subdivisions. The finer the subdivisions, the closer the resulting values are to the original values (the tradeoff will be that more simbols will be needed to express each subdivision)
To conclude, a digital signal is a series of numbers, obtained by sampling and quantizating an analog signal.
Numbers and symbols. Radix
As seen in the previous chapter, a digital signal is a series of values.
După cum s-a observat în capitolul anterior, un semnal digital este o înșiruire de valori. Aceste valori sunt reprezentate folosind simboluri, aparținând unei baze de numerație. Cel mai simplu exemplu este cel cu care suntem obișnuiți cu toții, adică baza zecimală, folosind ca simboluri cifrele de la 0 la 9. Dar acesta nu este nici pe departe singurul. Alte exemple ar fi sistemul de numerație roman, unde se folosesc ca simboluri literele I, V, X, L, C, D și M, unde valoarea acestor simboluri intr-un număr depinde de ordinea lor. Același lucru îl putem spune și despre baza de numerație zecimala, unde, spre exemplu, simbolul 9 are altă valoare dacă se află pe prima poziție (9) decât dacă se află pe a doua (90). Ce este interesant de reținut este că, în ciuda asocierii mentale dintre simbolurile cu care am fost obișnuiți de mici să lucrăm și valorile numerice pe care acestea le exprimă, cele două noțiuni sunt complet distincte. Valoarea „zece” poate fi exprimată numeric în baza zecimala ca 10, în sistemul de numerație roman ca X, în sistemul hexazecimal ca A, în sistemul binar ca 1010, în cel octal ca 12, dar toate aceste reprezentări exprimă, de fapt, același număr.
Sistemul de numerație binar
După cum îi spune și numele, acest sistem utilizează doar două simboluri, de cele mai multe ori, acestea fiind 0 și 1. Prin urmare, un număr poate fi reprezentat în sistemul binar (numit și baza 2) ca o secvență de 0 și 1. Ordinea simbolurilor într-un număr scris în baza doi respectă aceleași reguli ca și numerele scrise în baza zecimală. Astfel, daca într-un număr zecimal, cifra 7 pe poziția 4 era echivalentă cu valoarea 7 * 104, unde 10 este egal cu numărul de simboluri distincte folosite, atunci în baza 2, un 1 pe pozitia 4 este echivalent cu valoarea 1 * 24. Aceasta este și regula de transformare a numerelor din baza 2 în baza 10. Prin urmare:
1001010(2) = 1 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 64 + 0 + 0 + 8 + 0 + 2 + 0 = 54(10)
Transformarea unui număr din baza zecimală în cea binară implică împărțirea repetată la 2 (numărul de simboluri ale bazei), unde deîmpărțitul la fiecare iterație este dat de câtul împărțirii anterioare. Operația se repetă cât timp câtul este diferit de 0. Numărul în baza binară este dat de secvența resturilor începând cu ultima împărțire și terminând cu prima.
Avantajul sistemului binar este că numărul redus de simboluri face ca și numărul de operații posibile între două simboluri aleatoare să fie redus, prin urmare este ușor de imaginat o realizare fizică a unor circuite care să implementeze aceste operații. Dezavantajul este că pentru numere relativ mici, este nevoie de multe simboluri pentru reprezentare. Așadar, pentru flexibilitatea operației cu valori reprezentate cu multe simboluri, se utilizeaza baza de numerație hexazecimală, adică baza 16. După cum îi spune și numele, baza hexazecimală utilizează 16 simboluri: cifrele de la 0 la 9, și caracterele a, b, c, d, e și f. Utilizarea bazei 16 este avantajoasă datorită trecerii foarte ușoare între ea și baza 2. Astfel, la orice valoare reprezentată printr-o secvență de patru simboluri binare corespunde unul și numai un simbol hexazecimal.
Computație și control
Am ajuns deci la concluzia că se pot face calcule (computație) folosind doar două simboluri, corespunzătoare valorilor de zero și de unu. Avem la dispoziție o bază de numerație (baza doi), prin care se pot face calcule din cele mai complexe, cu aceeași acuratețe ca și cele din baza decimală. Dar pe lângă calculul efectiv, un sistem informatic trebuie să poată lua decizii, adică să poate evalua o expresie și să decidă valoarea acesteia de adevăr, operație de tipul general if then else. Cel mai simplu exemplu de funcție care nu se poate calcula fără luarea unei decizii, este funcția modul (de fapt, orice funcție cu ramuri). Aceasta este de forma:
if (operand < 0) then (result = -operand) else (result = operand);
Expresia (operand < 0) este ceea ce se numește o expresie logică. Expresiile logice, în algebra booleană, pot lua numai două valori: adevărat sau fals. Aceste valori pot fi notate cu aceleași simboluri pe care le utilizăm pentru valori numerice în baza doi, adică 0 pentru valoarea de adevăr fals (false) și 1 pentru valoarea de adevăr adevărat (true).
Cum asupra valorilor numerice pot fi aplicați operatori numerici (adunare, scădere, înmulțire), și asupra valorilor logice, pot fi aplicați operatori logici (ȘI, SAU, NU, SAU EXCLUSIV). Aceștia sunt explicați în detaliu pe pagina Wikipedia a algebrei booleane.
Concluzia este că folosind aceleași două simboluri, putem face calcule, folosind algebra binară, dar putem exercita control asupra unei funcții, folosind algebra booleană. După cum simbolurile se suprapun pentru computație și control, și operatorii asociați pot avea aceeași formă, și atunci distincția se face doar prin interpretarea lor. Spre exemplu, tabelul cu rezultate pentru înmulțirea a două numere de un bit (operație numerică) arată în felul următor:
| INTRARE | IEȘIRE | |
| A | B | A * B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
În același timp, operația logică ȘI care întoarce 1 dacă și numai dacă ambii operanzi sunt 1 (mă duc la film DACĂ nu plouă ȘI am bani), are următorul tabel de adevăr:
| INTRARE | IEȘIRE | |
| A | B | A ȘI B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Se observă că cele două funcții sunt identice. În acest fel, distincția dintre valoare logică și valoare numerică (respectiv operator logic și operator numeric) ține de interpretarea valorilor de intrare (dacă acestea sunt valori logice sau numerice) iar implementarea operatorilor este identică (prin urmare circuitul asociat este identic).
Circuits
In digital electronics, as in whole the digital circuit technology (computers) as in IT, an element that can have a binary value associated to a binary symbol is called bit. The basis of the digital circuits, however complex they may be, is given by its sub-circuits that compute unary and binary operations (one or two operands) using two bits. Such a circuit is called gate (en:gate). The same gate may be considered as an implementation of a bit operator (but also as a logic operator)
The way of coding the values associated to binary symbols, in digital electronics, is by a difference in potential between two points. In current technology (CMOS), a voltage between 0 and about Vdd/2 is associated to a binary value of 0 and a voltage between about Vdd/2 and Vdd, to a value of 1. [1]
One of the simplest gates is the one that implements the logical negation (has only one single input and one output that is always different than the input; that is, for the 0 input, the output is 1 and for the 1 input, the output is 0). This gate is called inverter, or NOT gate (en: inverter, NOT gate).
The symbols and the truth tables for the most used gates:
As in symbolic representation of the operational amplifiers, the gates also do not have the power lines drawn (Vdd and Vss), as they are visible in CMOS inverter. These are implicitly connected to the powerlines.
Verilog HDL
La ora actuală, un circuit digital poate ajunge până la 1 miliard de porți. Asta implică faptul că avem nevoie de unelte care să permită automatizarea procesului de design. Acest lucru se poate face folosind limbaje de descriere hardware (Hardware Description Languages). Aceste limbaje sunt special concepute pentru a putea descrie un circuit digital, ori din punct de vedere al comportamentului, ori din punct de vedere al structurii. În mod evident, o descriere comportamentală a unui circuit va fi mai succintă, dar nu va oferi informații despre structura dorită (la nivel de poartă), în timp ce o descriere structurală va fi mai exactă din punct de vedere al componentelor circuitului, dar mai lungă și poate mai dificil de înțeles.
Există două limbaje foarte cunoscute de descriere hardware: Verilog și VHDL. În continuarea acestui laborator de Circuite Integrate Digitale, vom folosi pentru descriere circuitelor, limbajul Verilog. Sintaxa acestuia este simplă și este parțial moștenită din C. Totuși, este foarte important de reținut că Verilog nu este un limbaj de programare. El nu se „execută” secvențial de către un procesor, ci se sintetizeaza într-un circuit sau se simulează. Prin urmare utilizatorii de Verilog trebuie să se dezobișnuiască să gândească secvențial ca și cum fiecare linie de cod se execută după cea precedentă, si mai degrabă trebuie să-și imagineze cum funcționează circuitul pe care codul respectiv îl descrie. Astfel, diferența cea mai interesantă față de un limbaj de programare, este că ordinea blocurilor de cod dintr-un modul nu contează.
Înainte de a începe lucrul cu uneletele software de simulare și sinteză, parcurgeți tutorial-ul care explică sintaxa Verilog.