DIC Seminar 6

In this seminar you will be presented the concept of finite automaton and how it is described in Verilog.

Keywords: finite automated, FSM (Finite State Machine), Mealy, Moore, state, transition Verilog syntax: localparam

The finite automaton, also called Finite State Machine (FSM), is a mathematical computation model, defined by the following elements:

• A finite set of input symbols, called input alphabet;
• A finite and unobserved set of exit symbols, called output alphabet;
• A finite and unobserved lot of states, of which only one, called the current state, is active at some point;
• An initial state, which is part of the set of states;
• A state transition function, which calculates the next state of the automaton according to the current state and the input symbol;
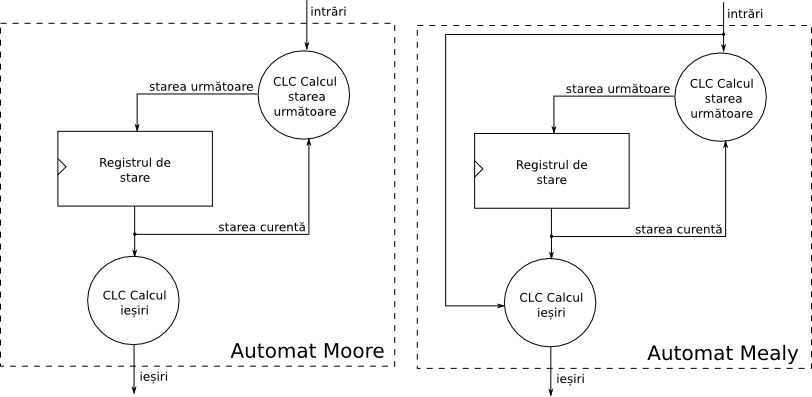
• An output calculation function, which determines the output symbol according to the current state (for Moore automata) or the current state and the input symbol (for Mealy machines).

In digital systems, a finite automaton is used to program a sequence of operations and can be implemented as a sequential circuit. Thus, the input and output symbols will be represented by all possible input and output combinations of the circuit. The state transition function and output calculus function will be implemented as combinational logic circuits (CLCs), and the current state of the automaton will be stored in an internal register.

At each clock front, the value of the next state, calculated by the CLC, will be loaded into the register. If the register has n bits, the maximum number of states that can be represented is 2 ⁿ . This number may be lower, depending on the status coding scheme. For example, for n=4, up to 16 states (0000, 0001, 0010, ..., 1111) can be represented by binary encoding, while for one-hot encoding, where only one bit can take the value 1, there may be 4 states (1000, 0100, 0010, 0001).

Question: Which is the easiest automatic you've ever met before?

States and transitions between them can be represented in different ways. The most used of these is the state diagram, in which the states and transitions are represented in the form of an oriented graph. Another possible way of representation is the state transition table, similar to a truth table.

Example 1

Define the necessary states and transitions for a finite automaton that recognizes the 0 ⁿ 1 ^m input sequence with n, m ≥ 0. Draw the state diagram. Describe the behavioral circuit in Verilog. Run a test module for this circuit.

What type of automatic did you implement?

Additional explanations:

The steps for describing the behavior of a finite automaton are as follows:

1. Analyze the requirement and draw the state diagram;
2. Count the states and set the number of bits you need for the status register;
3. Define the module in Verilog by adding inputs, outputs and internal status register;
4. Using a block always sequential and block conditional blocks, describe all possible transitions to other states for each possible state;
5. Define and describe combinational outputs according to current status and inputs.

Solution:

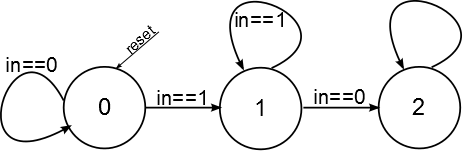
1. The machine will have 3 states: the initial state where 0 is waiting, the state it waits 1 and the error state when a value of 0 has been detected after the sequence 1. Thus, the state diagram is the following:

2. As the number of states is 3, we will need 2 bits for the status register.

3.

module FSM(
    input clock,
    input reset,
    input in,
    output detectOk,
    output detectFail
)

reg [1: 0] state;

always @ (posedge clock) begin
    if (reset) begin
        state <= 2'b00;
    end else begin
        case (state)
            2'b00: if (in == 1) state <= 2'b01;
            2'b01: if (in == 0) state <= 2'b10;
            2'b10:; //do nothing
            default: state <= 2'b00;
        endcase
    end
end

assign detectOk=(state == 2'b00) || (state == 2'b01);
assign detectFail=(state == 2'b10);

endmodule

module FsmTest;

reg clock;
reg reset;
reg in;
wire detectOk;
wire detectFail;

initial begin
    clock=0;
    forever #1 clock=~ clock;
end

initial begin
        in=0;
        reset=0;
    #2 reset=1;
    #2 reset=0;
    #6 in=1;
    #10 in=0;
    #10 $ stop ();
end

FSM dut (
    .clock (clock),
    .reset (reset)
    .in in),
    .detectOk (detectOk)
    .detectFail (detectFail)
)
   
endmodule

Notice that once you get into one of the final states, the machine crashes. In order to get back to the initial state, a reset signal is required. Thus:

Rule: A finite automate necessarily has a reset port. When the reset is active, the machine switches to one of the states, which is so designated as the initial state.

Notice that we have an unused state. Generally, as a rule of good practice, for all unused states, which are the case default in the house block, the next transition will always be to the initial state (reset).

Notice that states are defined as values. For a large number of states, the codes will become difficult to understand. Therefore, we introduce the following notations in the mode:

localparam STATE_READ_0=2'b00;
localparam STATE_READ_1=2'b01;
localparam STATE_ERROR=2'b10;

These notations can then be used instead of the values:

always @ (posedge clock) begin
    if (reset) begin
        state <= STATE_READ_0;
    end else begin
        houses (state)
            STATE_READ_0: if (in == 1) state <= STATE_READ_1;
            STATE_READ_1: if (in == 0) state <= STATE_ERROR;
            STATE_ERROR:; //do nothing
            default: state <= STATE_READ_0;
        endcase
    end
end

assign detectOk=(state == STATE_READ_0) || (state == STATE_READ_1);
assign detectFail=(state == STATE_ERROR);

Example 2

Describe structurally the module from the previous example as follows:

• The two CLCs will be defined as separate modules;
• "The machine will be a" top "module in which you instantiate the two CLCs and the status register."

Test the machine with the test module from the previous exercise.

Example 3

Make a finished machine for a car that sells CMOS chocolate, which costs $ 2.5. The machine accepts coins of 50 bani and 1 leu banknotes. Name the current status based on the currently accumulated amount, expressed in multiples of 50 bani (for example STATE_0_BANI, STATE_50_BANI, STATE_100_BANI, etc.). When the amount of 2.5 lei or more is reached, the machine will deliver a chocolate and will resume the process, lowering 2.5 lei from the current amount. The machine does not return the change.

What type of automatic did you implement?

Additional explanations:

The circuit must have the following ports:

• input load50bani - active when a 50-dollar coin is introduced
• input load1leu - active when a 1 leu banknote is entered
• output ack50bani - active when the machine detects the insertion of a 50-dollar coin
• output ack1leu - active when the machine detects the insertion of 1 leu banknote
• output productDelivered - active when a chocolate is delivered

Why are the 'ack' ports needed?

Example 4

If one or more of the machine's inputs are asynchronous (it changes its value independently of the clock clock), then the state register entry can also change its asynchronous value. Thus, to avoid transition in an undefined state, or a state in which the machine should not come as usual, all states are coded so that between code current status code next state differ in only one bit. This coding mode is called Gray Code.

In our first example, we had 3 states:

• STATE_READ_0, encoded 2'b00
• STATE_READ_1, encoded 2'b01
• STATE_ERROR, encoded 2'b10

It can be noticed here that the STATE_ERROR state is adjacent to state STATE_READ_1, but their coding differs by both bits, so it is not a Gray code. If, say, we are in the STATE_READ_1 state (2'b01) and the input of the machine is 1, then the CLC that calculates the next state will output 2'b01. But when the input of the machine changes to 0, then this change propagates through gates to the output of the CLC, changing its value to 2'b10 (error state). Yet we know that these two signals can not reach exactly the same time, so perhaps the least significant bit to change the first case in which, for a very short time, CLC's output will be 2'b00 up when it reaches the correct value of 2'b10. Similarly, the most significant bit can be changed first, leading to the value in 2'b11 until it stabilizes again in 2'b10. In both these cases, if the wrong value is stored in the status register, this implies a transition erroneous times in STATE_READ_0 STATE_READ_1 state or invalid state 2'b11.

We can restore the status codes as follows:

• STATE_READ_0, encoded 2'b00
• STATE_READ_1, encoded 2'b01
• STATE_ERROR, encoded 2'b11

Analyze possible transitions due to asynchronous input. What do you notice?

Perform a 4-bit Gray counter so that any two consecutive values can be fixed by one bit. Write a test module for this circuit to verify that it behaves correctly.

Homework

Modify the machine from example 3 so that it can return the change.