CID aplicatii 5 : Exercitii cu circuite combinationale
Teorie
Acest laborator are rolul de a sedimenta cunostiintele dobandite anterior.
El consta in exercitii separate, unele date ca subiect la lucrarea 1 in anii anteriori si cateva notiuni de teorie si sintaxa ajutatoare.
Teorie: Parametrizare
Parametrizarea este un mod de a generaliza codul scris pentru a nu fi nevoie sa scrii acelasi modul de mai multe ori doar pentru ca circuitul isi schimba o dimensiune.
Pentru a intelege mai clar avantajele si sintaxa urmariti urmatorul exemplu:
Fisierul sumator.sv:
module sumator # // <= diez deoarece urmeaza lista cu paramteri
( // parametri
parameter data_size = 4 // valoare default 4
// alti parametri aici daca este nevoie, separati prin virgula
)
( // interfata
input logic [data_size-1:0] in0, // si pot folosii parametrul "data_size" pentru dimensiunea bus-ului
input logic [data_size-1:0] in1,
output logic [data_size-1:0] out0
);
assign out0 = in0 + in1;
endmodule
Cand se instantiaza un modul parametrizat, se specifica valorile parametrilor astfel:
sumator # ( // parametri
.data_size(8) // se genereaza un sumator pe 8b
)
nume_instanta_0
( // interfata
.in0(fir_in0),
.in1(fir_in1),
.out0(fir_out0)
);
sumator # ( // parametri
.data_size(32) // se genereaza un sumator pe 32b
)
nume_instanta_1
( // interfata
.in0(fir_in0),
.in1(fir_in1),
.out0(fir_out1)
);
sumator nume_instanta_2 // se genereaza un sumator de dimensiune default, aici 4, asa cum e scris in modulul "sumator"
( // interfata
.in0(fir_in0),
.in1(fir_in1),
.out0(fir_out2)
);
Puteti folosi parametrizarea in exercitiul 3 de mai jos. Acolo sunt 2 tipuri de multiplexoare, unul cu intrarile pe 1 bit si unul cu intrarile pe 2 biti. Poate fi scris un singur modul parametrizat care sa acopere ambele situatii.
Teorie: Concatenarea
Pentru o mai usoara conectare a firelor sau pentru o mai buna organizare si expresivitate a codului, de multe ori este util ca fire individuale sa fie grupate impreuna sau ca un bus de mai multi biti sa fie separat in fire individuale. Acest lucru se face folosind concatenarea, prin simbolurile "{ }".
Un exemplu de folosire a concatenarii este oferit mai jos. Un sumator pe 8b are rezultatul pe maxim 9b, in cazul in care ambele numere sunt mari. Astfel apare un bit de carry out.
module sumator (
input logic [7:0] in0,
input logic [7:0] in1,
output logic [7:0] out0,
output logic carry_out
);
assign {carry_out,out0} = in0 + in1; // fac suma intre in0 si in1 iar rezultatul il pun pe cei 9b alcatuiti din: 1b carry_out si 8b out0, in ordinea asta
endmodule
Se pot concatena oricat de multe semnale, puse in "{ }" si separate prin virgula. Atentie la dimensiunile firelor care se concateneaza.
Se poate de asemenea face concatenare si la dreapta egalului, astfel:
assign fir_pe_10_b = {fir_pe_3b,fir_pe_5b,fir_pe_1b,fir_pe_1b};
In exemplul anterior ultimi 2b ai "fir_pe_10_b" vor avea mereu aceeasi valoare, provenind din acelasi fir. Sintaxa SystemVerilog permite asta.
Puteti folosii concatenarea, in exercitiul 2, la flag-ul de overflow.
Teorie: Constante ca intrari in circuite
In cazul in care se doreste scrierea unor constante la intrarea unor module, acestea se pun direct intre paranteze la instantiere. De exemplu, pentru multiplexorul de jos din subiectul "alu structural", intrarea "in3" este conectata la valoarea "1". Sintaxa pentru aceasta este: ".in3(1),".
Teorie: "_"
Simbolul "_" (underscore) este ignorat de SystemVerilog si ajuta vizual la citirea semnalelor pe mai multi biti. De exemplu 16'b1010010111110000 este identic cu 16'b1010_0101_1111_0000, al doilea fiind totusi mai usor de citit.
Exercitii
Exercitiul 0: Repararea erorilor
Arhiva de mai jos contine mai multe proiecte in Vivado, fiecare avand cate o eroare de sintaxa sau de logica. In vederea aprofundari cunostiintelor voastre (si pentru lucrarea de saptamana urmatoare), incercati sa le parcurgeti si sa rezolvati toate problemele. Pe langa proiecte in sine, in arhiva se afla si un fisier text cu o introducere, rezolvarile si explicatiile pentru fiecare situatie.
Exercitiul 1: ALU - descriere comportamentala
Descrieți comportamental o unitate aritmetico-logică (ALU) care are la intrare 2 numere binare de câte 8 biți și poate calcula următoarele funcții:
- - suma celor două numere
- - diferența celor două numere
- - operații logice bit cu bit (bitwise): SI, SAU, XOR și inversele lor
- - operandul din stanga trece neschimbat
- - operandul din dreapta trece neschimbat
- - numărul din stânga este deplasat la stânga cu nr. de poziții indicat de numărul din dreapta
- - numărul din stânga este deplasat la dreapta cu nr. de poziții indicat de numărul din dreapta
Funcția executată la un anumit moment este determinată de configurația binară de pe intrarea de comandă (function).
ALU are de asemenea intrare de carry și ieșire de carry, plus alte două ieșiri - indicatori - pentru cazurile când rezultatul este zero și când cei doi operanzi sunt egali.
Intrarea de control va fi facuta pe 4 biti ca sa permita existenta a 16 operatii posibile. Fiecare numar de pe intrarea de control (combinatie de 0 si 1) va reprezenta o operatie din cele de mai sus. Scrierea se va face folosind un bloc "case" in functie de aceasta intrare.
Exercitiul 2: ALU - descriere structurala
Daca se doreste selectarea doar a anumitor biti dintr-un bus (cum se vrea din instruction) acest lucru se poate face in 2 feluri:
a) cu fir aditional:
- wire [1:0] fir_aditional1;
- assign fir_aditional1 = instruction[11:10];
- // apoi la instantiere: .sel(fir_aditional1),
b) direct in instantiere;
- la instantierea celor 2 mux4 din stanga, direct:
- .sel(instruction[11:10]),
Pentru a scrie mai putin (a nu face toate modulele de calcul separat + instantierea lor) si pentru ca e vorba de operatii simple, se poate pune operatia cu assign direct in top pe un fir declarat acolo, sau si mai prescurtat, direct operatia dorita cand se intantiaza modulul in care aceasta intra. De exemplu, pentru operatia de shift la dreapta care intra in primul multiplexor, se poate pune: ".in0(data0 >> data1),".
Exercitiul 3: Multiplexoare
Exercitiul 4: Rom/Look-up table
Exercitiul 5: Sumator cu reprezentare in cifre zecimale
Proiectati si verificati un sumator zecimal pentru numere cu 2 cifre
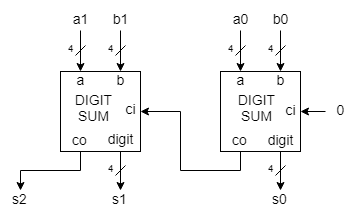
Modulul de top (Figura 1) este alcatuit din 2 blocuri de tip digitsum. Fiecare bloc aduna cifrele de pe aceasi pozitie.
Figura 1
Top level
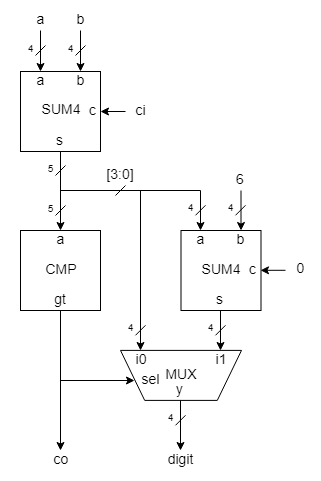
Blocul digitsum (Figura 2) este alcatuit din 4 blocuri, 2 sumatoare binare pe 4 biti (de tip sum4), o instanta de cmp si un multiplexor elementar mux2
Figura 2
Blocul DIGIT SUM
Primul sumator aduna cifrele din domeniul [0...9] avand un rezultat intre [0 ... 18]
Comparatorul are la iesire 1 daca rezultatul este mai mare decat 9.
Daca rezultatul este mai mic decat 9, acesta este trimis in mod direct la iesirea digit a blocului digitsum.
Daca rezultatul este mai mare decat 9, o crectie este necesara si se aduna 6 la rezultat.
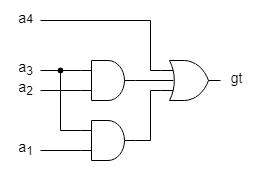
Comparatorul cu valoarea 9 este descris structural din porti in figura de mai jos:
Figure 3
the comparator
Testbench-ul va genera stimuli pentru bcdsum ca in Figura 4.
Intrarea b0 a bcdsum se schimba la fiecare 5 pasi de simulare .
b1, a0 si a1 se schimba sincron cu b0 ca in Figura 4.
Figure 4
Cerinte:
- cmp- descris structural la nivel de porti ca in Figura 3.
- sum4 descris comportamental cu un assign continuu.
- mux descris comportamental cu always.
- digitsum descris strctural ca in Figura 2.
- modulul de top numit bcdsum, descris structural ca in Figure 1.
- modulul de testbench, bcdsum_tb, instantiaza bcdsum cu numele dut.
- in testbench, generati stimuli pentru intrarile circuitului testat.