ED aplicatii 2 : Exercitii cu circuite combinationale si generare forme de unda
În această sesiune de aplicații vom învăța cum să generăm semnale digitale cu ajutorul limbajului Verilog. Generarea de semnale este utilizată în testarea prin simulare a circuitelor digitale. Semnalele generate sunt introduse la intrarea circuitului, observându-se apoi cum se modifică starea ieșirilor acestuia.
Proiectarea circuitelor digitale se bazează pe generarea unor circuite digitale fizice. Deși se va scrie cod în limbajul Verilog, mereu trebuie avut în vedere faptul că în spate se va genera un circuit fizic, codul nu se rulează pas cu pas, aceasta fiind deosebirea fundamentală dintre limbajele de descriere hardware (generează circuite fizice) și limbajele de programare (cod care se execută pas cu pas). Unele concepte cât și unele elemente de sintaxa este posibil să semene cu ce ați facut la programare, dar este important să înțelegeți că prin codul scris se desenează/generează circuite. Sau invers, pornind de la un desen, se poate face o descriere în Verilog a acestuia.
Proiectele exemplu care pot fi descărcate au fost implementate folosind Vivado 2021.2. Dacă aveți altă versiune este posibil să vă ceară să le salvați în versiunea respectivă sau să fie nevoie să vă faceți un proiect nou, în care să adaugați fișierele cu cod.
Noțiuni și cunoștințe necesare
- Introducere. Verilog HDL (Sintaxa Verilog)
Modulul de test (Testbench)
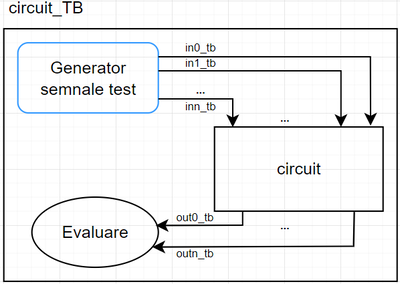
Modulul de test este un modul nesintetizabil (nu poate fi transformat într-un circuit de către utilitarul care realizează sinteza) și este folosit, așa cum sugerează și numele, în testarea circuitelor. Acest modul este folosit exclusiv în simulare. Simularea permite detecția rapidă a erorilor de implementare și corectarea acestora. Ideea generală a unui modul de test este descrisă în figura de mai jos (considerăm un circuit cu numele circuit și modulul său de test circuit_tb):
După cum se vede în figura de mai sus, modulul de test conține printre altele și un generator de semnale de test. Acesta are rolul de a genera câte un semnal de test pentru fiecare intrare a circuitului. Forma acestor semnale de test este stabilită de către cel care realizează verificarea și trebuie aleasă astfel încât să detectăm cât mai multe posibile erori.
Exemple
Exemplul 1: Generarea a doua semnale digitale de 1 bit
Să se genereze două semnale digitale de 1 bit, care să aibă următoarea variație în timp (unitatea de timp este de 1ns):
`timescale 1ns/1ps // setăm unitatea de timp la 1ns, cu o precizie de 1ps
module waveform1(); // modulul se numește waveform1 și nu are nicio intrare și nicio ieșire. Semnalele de test generate sunt semnale interne.
reg a, b; // cele două semnale de test sunt modificate într-un bloc de tip initial și trebuie declarate ca elemente de tip reg.
initial begin
$monitor("time = %2d, a = %b, b=%b", $time, a, b); // monitorizăm în consolă starea semnalelor a si b
a = 0; // semnalul a va avea valoarea 0 la momentul inițial de timp (la momentul t = 0)
b = 0; // semnalul b va avea valoarea 0 la momentul inițial de timp (la momentul t = 0)
#1 a = 1; // după 1ns de la momentul inițial, a se face 1
#1 b = 1; // după 2ns de la momentul inițial, b se face 1
#1 a = 0; // după 3ns de la momentul inițial, a se face 0
b = 0; // după 3ns de la momentul inițial, b se face 0
#2 $stop(); // simularea este oprită
end
endmodule // incheiem descrierea modulului de generare de semnale digitale
Observație: Atunci când un semnal are dimensiunea de 1 bit, nu va apărea nimic intre tipul acestuia și nume. Atunci când semnalul are o dimensiune mai mare sau egală cu doi biți, dimensiunea va fi descrisă sub forma [n-1:0], unde n este numărul de biți. Conform acestei descrieri, bitul n-1 este cel mai semnificativ.
reg a; //semnal cu dimeniunea de 1 bit
reg [7:0] data; //semnal/magistrală/bus cu dimensiunea de 8 biți
Exemplul 2: Generarea unui semnal periodic de 1 bit
Să se genereze un semnal digital periodic de 1 bit, cu perioada egală cu 2ns:
`timescale 1ns/1ps // setăm unitatea de timp la 1ns, cu o precizie de 1ps
module waveform2(); // modulul se numește waveform2 si nu are nicio intrare și nicio iesire
reg clock; // semnalul de test se va modifica într-un bloc initial, așadar este declarat de tip reg
initial begin
clock = 0; // valoarea inițială a semnalului va fi 0 (la momentul t = 0)
forever #1 clock = ~clock; // forever indică faptul că ce urmează se va repeta într-o buclă continuă.
// La trecea unui timp egal cu unitatea de timp definită, semnalul clock iși va nega valoarea
end
initial begin
#20 $stop(); // La 20 de unități de timp (aici, 20 ns), simularea se va opri.
// Aici punem $stop într-un bloc separat, deoarece forever blochează blocul initial în care se află
// Toate blocurile initial încep la același moment de timp (t = 0) și au efect în paralel
end
endmodule
Exerciții
Exercițiul 1
Generați două semnale digitale a și b de 1 bit, astfel încât să se formeze cu ele toate cele 4 combinații posibile, după cum urmează:
t = 0ns: a = 0, b = 0 t = 1ns: a = 0, b = 1 t = 2ns: a = 1, b = 0 t = 3ns: a = 1, b = 1
Exercițiul 2
Să se genereze un semnal digital de 8 biți aliniat la fronturile crescătoare ale unui semnal periodic (semnal de ceas), ce are perioada de 2ns:
Observație:
- Frontul crescător al unui semnal este definit ca tranziția dintre nivelul de 0 logic și 1 logic.
- Spunem că un semnal este aliniat la fronturile crescătoare ale unui alt semnal dacă acesta își modifică valoarea imediat după apariția acelui front crescător. În figura de mai sus, se observă că data își schimbă valoarea imediat după fiecare front crescător al semnalului clock.
Indicații:
- Așteptarea unui front crescător al semnalului NumeSemnal se realizează cu @(posedge NumeSemnal). Aceasta va înlocui întârzierile de tip #n folosite anterior.
- Pentru semnalele ce se doresc aliniate la un eveniment de tip posedge, vom folosi atribuirea non-blocantă: de exemplu, data <= 1;.
- Nu uitați! Folosirea forever pentru generarea semnalului de ceas va bloca acel bloc initial.
- Incrementarea valorii unui semnal se poate realiza cu un bloc de tip for, inclus in blocul initial. Blocul for va avea nevoie de un contor de tip integer, declarat în afara blocului initial. Pentru mai multe detalii, consultați tutorialul de sintaxa Verilog.
Folosind indicațiile anterioare, înlocuiți al doilea bloc initial din Exemplul 2 cu următoarea secvență și completați liniile de cod lipsă:
integer index;
initial begin
for(index = 0; index < 11; index = index + 1) begin
//completati codul
end
#20 $stop();
end
Exercițiul 3
Desenați formele de undă ale semnalelor de test a, b și c, generate cu ajutorul următoarelor două blocuri initial:
`timescale 1ns/1ps
module waveform();
reg a, b, c;
initial begin
a = 0;
b = 0;
#2 b = 1;
#1 a = 1;
#3 b = 0;
#3 a = 0;
#2 $stop();
end
initial begin
c = 1;
#2 c = 0;
#3 c = 1;
end
Exercițiul 4
Generati un semnal digital clock cu dimensiunea de 1 bit si perioada de 2ns si un semnal digital data, cu dimensiunea de 4 biti, aliniat la fronturile crescatoare ale semnalului clock. Semnalul data va varia astfel: 0, 1, 2, 3, 0, 1, 2 ,3, 0, 1 ... . Opriti simularea dupa ce semnalul data a realizat 4 variatii complete (s-a generat secventa 0, 1, 2, 3 de 4 ori).
Teorie
Acest laborator are rolul de a sedimenta cunostiintele dobandite anterior.
El consta in exercitii separate, unele date ca subiect la lucrarea 1 in anii anteriori.
Teorie: Parametrizare
Parametrizarea este un mod de a generaliza codul scris pentru a nu fi nevoie sa scrii acelasi modul de mai multe ori doar pentru ca circuitul isi schimba o dimensiune.
Pentru a intelege mai clar avantajele si sintaxa urmariti urmatorul exemplu:
Fisierul sumator.v:
module sumator # // <= diez ca sa stie ca urmeaza lista cu paramteri
( // parametri
parameter data_size = 4 // valoare default 4
// alti parametri aici daca este nevoie, separati prin virgula
)
( // interfata
input wire [data_size-1:0] in0, // si pot folosii parametrul "data_size" pentru dimensiunea bus-ului
input wire [data_size-1:0] in1,
output wire [data_size-1:0] out0
);
assign out0 = in0 + in1;
endmodule
Cand se instantiaza un modul parametrizat, se specifica valorile parametrilor astfel:
sumator # ( // parametri
.data_size(8) // se genereaza un sumator pe 8b
)
nume_instanta_0
( // interfata
.in0(fir_in0),
.in1(fir_in1),
.out0(fir_out0)
);
sumator # ( // parametri
.data_size(32) // se genereaza un sumator pe 32b
)
nume_instanta_1
( // interfata
.in0(fir_in0),
.in1(fir_in1),
.out0(fir_out1)
);
sumator nume_instanta_2 // se genereaza un sumator de dimensiune default, aici 4, asa cum e scris in modulul "sumator"
( // interfata
.in0(fir_in0),
.in1(fir_in1),
.out0(fir_out2)
);
Puteti folosi parametrizarea in exercitiul 3 de mai jos. Acolo sunt 2 tipuri de multiplexoare, unul cu intrarile pe 1 bit si unul cu intrarile pe 2 biti. Poate fi scris un singur modul parametrizat care sa acopere ambele situatii.
Teorie: Concatenarea
Pentru o mai usoara conectare a firelor sau pentru o mai buna organizare si expresivitate a codului, de multe ori este util ca fire individuale sa fie grupate impreuna sau ca un bus de mai multi biti sa fie separat in fire individuale. Acest lucru se face folosind concatenarea, prin simbolurile "{ }".
Un exemplu de folosire a concatenarii este oferit mai jos. Un sumator pe 8b are rezultatul pe maxim 9b, in cazul in care ambele numere sunt mari. Astfel apare un bit de carry out.
sumator (
input wire [7:0] in0,
input wire [7:0] in1,
output wire [7:0] out0,
output wire carry_out
)
assign {carry_out,out0} = in0 + in1; // fac suma intre in0 si in1 iar rezultatul il pun pe cei 9b alcatuiti din: 1b carry_out si 8b out0, in ordinea asta
endmodule
Se pot concatena oricat de multe semnale, puse in "{ }" si separate prin virgula. Atentie la dimensiunile firelor care se concateneaza.
Se poate de asemenea face concatenare si la dreapta egalului, astfel:
assign fir_pe_10_b = {fir_pe_3b,fir_pe_5b,fir_pe_1b,fir_pe_1b};
In exemplul anterior ultimi 2b ai "fir_pe_10_b" vor avea mereu aceeasi valoare, provenind din acelasi fir. Sintaxa Verilog permite asta.
Puteti folosii concatenarea, in exercitiul 2, la flag-ul de overflow.
Exercitii
Exercitiul 1: ALU - descriere comportamentala
Descrieți comportamental o unitate aritmetico-logică (ALU) care are la intrare 2 numere binare de câte 8 biți și poate calcula următoarele funcții:
- - suma celor două numere
- - diferența celor două numere
- - operații logice bit cu bit (bitwise): SI, SAU, XOR și inversele lor
- - operandul din stanga trece neschimbat
- - operandul din dreapta trece neschimbat
- - numărul din stânga este deplasat la stânga cu nr. de poziții indicat de numărul din dreapta
- - numărul din stânga este deplasat la dreapta cu nr. de poziții indicat de numărul din dreapta
Funcția executată la un anumit moment este determinată de configurația binară de pe intrarea de comandă (function).
ALU are de asemenea intrare de carry și ieșire de carry, plus alte două ieșiri - indicatori - pentru cazurile când rezultatul este zero și când cei doi operanzi sunt egali.
Intrarea de control va fi facuta pe 4 biti ca sa permita existenta a 16 operatii posibile. Fiecare numar de pe intrarea de control (combinatie de 0 si 1) va reprezenta o operatie din cele de mai sus. Scrierea se va face folosind un bloc "case" in functie de aceasta intrare.
Exercitiul 2: ALU - descriere structurala
Daca se doreste selectarea doar a anumitor biti dintr-un bus (cum se vrea din instruction) acest lucru se poate face in 2 feluri:
a) cu fir aditional:
- wire [1:0] fir_aditional1;
- assign fir_aditional1 = instruction[11:10];
- // apoi la instantiere: .sel(fir_aditional1),
b) direct in instantiere;
- la instantierea celor 2 mux4 din stanga, direct:
- .sel(instruction[11:10]),
Exercitiul 3:
Exercitiul 4:
Exercitiul 5: Sumator cu reprezentare in cifre zecimale
Proiectati si verificati un sumator zecimal pentru numere cu 2 cifre
Modulul de top (Figura 1) este alcatuit din 2 blocuri de tip digitsum. Fiecare bloc aduna cifrele de pe aceasi pozitie.
Figura 1
Top level
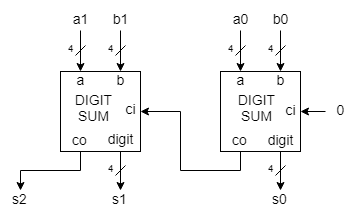
Blocul digitsum (Figura 2) este alctuit din 4 blocuri, 2 sumatoare binare pe 4 biti (de tip sum4), o instanta de cmp si un multiplexor elementar mux2
Figura 2
Blocul DIGIT SUM
Primul sumator aduna cifrele din domeniul [0...9] avand un rezultat intre [0 ... 18]
Comparatorul are la iesire 1 daca rezultatul este mai mare decat 9.
Daca rezultatul este mai mic decat 9, acesta este trimis in mod direct la iesirea digit a blocului digitsum.
Daca rezultatul este mai mare decat 9, o crectie este necesara si se aduna 6 la rezultat.
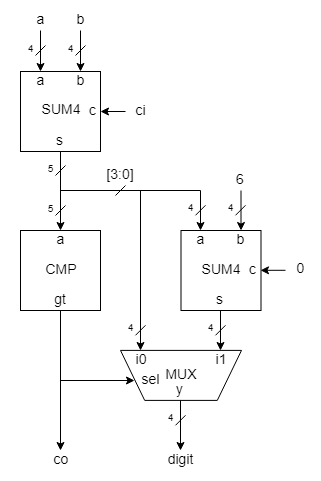
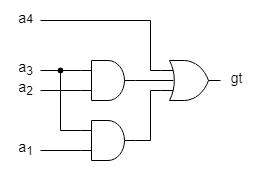
Comparatorul cu valoarea 9 este descris structural din porti in figura de mai jos:
Figure 3
the comparator
Testbench-ul va genera stimuli pentru bcdsum ca in Figura 4.
Intrarea b0 a bcdsum se schimba la fiecare 5 pasi de simulare .
b1, a0 si a1 se schimba sincron cu b0 ca in Figura 4.
Figure 4
Cerinte:
- cmp- descris structural la nivel de porti ca in Figura 3.
- sum4 descris comportamental cu un assign continuu.
- mux descris comportamental cu always.
- digitsum descris strctural ca in Figura 2.
- modulul de top numit bcdsum, descris structural ca in Figure 1.
- modulul de testbench, bcdsum_tb, instantiaza bcdsum cu numele dut.
- in testbench, generati stimuli pentru intrarile circuitului testat.