Verilog EN
Modules (synthesizable)
The Verilog language is structured on modules. Each module represents a circuit that implements a certain function. For example, a module may be a summation, ie a circuit that has two entries specifying the two operands and an output representing the result of the assembly. The content of the module is the (structural or behavioral) description of the gates that calculate the sum of the two entries. Therefore, the definition of a Verilog module has two parts:
- interface - the list of all the input and output ports of the circuit, specified by name and size;
- implementation - actual circuit description using input values to calculate output values;
Verilog Module Interface
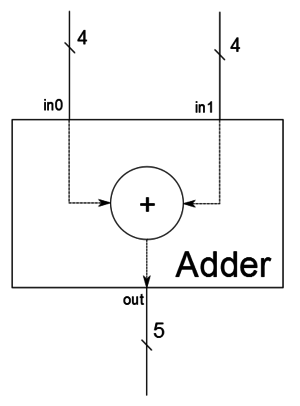
The Adder module interface is shown below. Note: As in the decimal system, where the sum of two numbers n digits needs n+1 digits ( 9 + 9 = 18), in the binary system, the sum of two n bits will be on n + 1 bits.
module Adder (
output [4: 0] out,
input [3: 0] in0,
input [3: 0] in1
);
//implementation
endmodule
The keywords module and endmodule are used to start and end defining a module. Immediately after the keyword module follows the module name.
Convention: The name of a module will begin with a large letter.
After defining the module name, the list of ports, placed between round brackets and separated by comma follows. Accepted keywords are output (representing an output port), input (representing an input port) and ' 'inout' '(representing a bidirectional port).
Tip: Introduction of Tri-state Buffer elements is ineffective. A more efficient alternative is to define two ports, one input and one output, with similar names (ex: data_in and data_out ).
Convention: First the outputs, then the inputs of a module are defined.
Convention: module.
According to the port type, it follows its size, specified in the bit indexes, where the least significant bit has the index 0. For example, a 4 bit signal will have the following specification: [3: 0] significantly has index 3, least significant 0, total 4 bits). Note: One-bit signals lack the size specification:
input signal_de_un_bit,
After the list of ports in brackets, the interface definition ends with the ; character.
- Remark: There are non-synthesizable modules (which do not have logical gaps), which are used as test programs in simulation environments and are called test modules. These modules have no input and output ports and are used only to give the input port values of the module to be tested, and to check the values on the output ports of the module. For these modules, the list of ports and their associated parentheses are missing:
Module TestModule;
//implementation
endmodule
Implementing Verilog Modules
The implementation of Verilog modules is done through blocks. These blocks may or may not correspond to a physical scent. If all blocks of a module have a correspondent in a physical circuit, then the module is synthesizable and can be transformed into a physical circuit. Blocks that can generate synthesizable constructions are of four types:
- blocks assign
- blocks always
- Instance blocks
- blocks generated
In addition, Verilog can define threads (wire) and registers (reg).
Blocks that are always unintelligible and are used exclusively for simulation:
- blocks initial
Remark: Not all assign or always blocks are synthesizable. There are syntactic constructs that do not have a correspondent in the circuit. These blocks can be simulated but can not be used to program an FPGA
Note: The order of blocks in a module does not matter.
Fire (wire) and registers (reg)
The threads are used for linking modules and for assigning partial results to combinational circuits, therefore:
Rule: or as the output of a module (never both simultaneously).
The threads in a Verilog module are defined as follows:
wire [3: 0] bunch_of_wires;
Registers are commonly used to implement sequential circuits, and in those circuits they are physical registers, but:
Remark: A reg element does not necessarily translate into a physical register. Translating it depends on how it is used.
A register is defined as follows:
reg [3: 0] register;
Rule: or initial.
Rule: No element can change its value in more than one block. That is, for a wire ( wire ), there can not be two assign blocks in which it changes the value, and for reg there is only one block of always or initial in which it changes its value.
Note: An input of a module is always a wire. Therefore the statement
input [3: 0] in0,
is equivalent to
input wire [3: 0] in0,
Remark: An output of a module may be a wire or reg. If not specified, it is a wire type. Therefore the statement
output [4: 0] out,
is equivalent to
output wire [4: 0] out,
assign blocks
assign is a key word that generates combinational circuits. As the summator is a combinational circuit, and output is implicitly wire type, we can implement it with a block assign
module Adder (
output [4: 0] out,
input [3: 0] in0,
input [3: 0] in1
);
assign out=in0 + in1;
endmodule
Note: Generally, a block assign will generate a synthesizable circuit. There are also exceptions when the desired operation is too complex to be implemented through a combinational circuit effectively. E.g:
assign out=in0 /in1;
is not a synthesizable code for most synthesis tools, but works fine in a simulation.
Combinational always blocks
Always, a block always is used to give values of reg signals. A block always may translate into [combinational circuits]] or sequential circuits, depending on its list of sensitivities. The general format for a always block is the following:
always @ (<sensitivity list>) begin
//...
end
As the name calls it, the list of sensitivities is the list of sensitive signals, that is, the registers described by the block always depend on. If only the name of a signal is passed in the list of sensitivities without any additional specifiers, then the block is sensitive to any change of this signal. If a block always has more signals to which it is sensitive, they split into the sensitivity list using the keyword or.
Note: If the list of sensitivities contains only signals without other specifiers, then the result of the block synthesis will be a combinational circuit.
In this case, we can redo the implementation of the summator using a block always as follows:
module Adder (
output reg [4: 0] out,
input [3: 0] in0,
input [3: 0] in1
);
always @ (in0 or in1) begin
out=in0 + in1;
end
endmodule
always sequential blocks. Non-blocking assignments
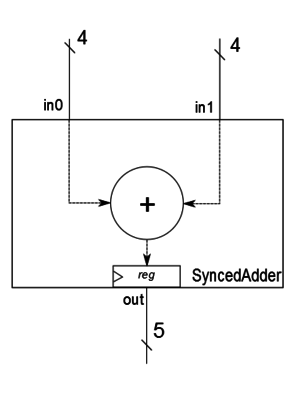
Sequential Circuits are circuits that are synchronized by [Sequence Circuits #Clock Signal | Clock Signal]. This signal is usually produced by a clock generator and is defined as input for each sequential module (in which there is at least one register). We can modify the previous example so that the output of the summation module is synchronous (that is, change only on the positive clock front). Thus, in the module interface, the clock signal also appears:
module SyncedAdder (
output reg [4: 0] out,
input [3: 0] in0,
input [3: 0] in1,
input clock
);
//implementation here
endmodule
Rule: Always use a always block to describe sequential circuits.
Block always that describes a sequential circuit has only the clock signal in the list of sensitivities and it is not sensitive to any clock transition but only to one of the fronts (usually the positive one). Thus, we can implement the Synchronizer as follows:
module SyncedAdder (
output reg [4: 0] out,
input [3: 0] in0,
input [3: 0] in1,
input clock
);
always @ (posedge clock) begin
out <= in0 + in1;
end
endmodule
Note: The key word that specifies the positive front of a signal is posedge and the negative signal side is negedge.
Note the operator <= used to assign the amount of the target register. It is NOT the 'less than or equal' logical operator, but it is an assignment mode called non-blocking. The difference between blocking assignment (=) and non-blocking (<=) is that the second one evaluates all the expressions on the right hand side of the assignment operator front, sum in0 + in1 ) and only then assigns the result of the destination registry. For example, if we want to invert the values of two registers, 'reg0' and 'reg1', so that 'reg0' takes the value of 'reg1' and vice versa, we will do the following:
module RegSwapper (
//...
);
reg [31: 0] reg0;
reg [31: 0] reg1;
//correct code
always @ (posedge clock) begin
reg0 <= reg1;
reg1 <= reg0;
end
endmodule
The module will behave as expected. The operator <= will not block the rest of the always block evaluations and therefore all assignments are made simultaneously after evaluating the operator's right-hand expressions. On the other hand, if we do the blocking assignment:
module RegSwapper (
//...
);
reg [31: 0] reg0;
reg [31: 0] reg1;
//incorrect code
always @ (posedge clock) begin
reg0=reg1;
reg1=reg0;
end
endmodule
this will block the rest of the operations until the assignment ends. In this case, after the first clock queue, both registers will contain the initial value of reg1 .
The non-blocking assignment operator (<=) is used only in blocks always or initial.
Rule: In the same block always, the same type of assignment operator is used for all operations.
Use non-blocking assignment for all blocks always which generate sequential circuits (are clock synchronized) and blocking assignment in all other cases.
Instantiation blocks
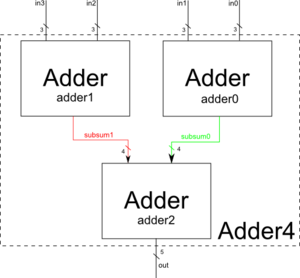
Once a module is defined, it can be used anytime during one or more projects. This system is called instantiation. Let's take as an example a module that has to make the sum of 4 3-bit numbers. We can use for this purpose the 4-bit Adder 'module as defined above, in the configuration in the figure. Notice that the same module is used three times. It's inefficient and useless to write the implementation of the module three times, so we'll resort to the instantiation method. Any instance of a module must have a unique name, as in a programming language, the same kind of variables must have a unique name.
It is further noted that there are "threads" in the Adder4 module that are neither input nor output and are used only to connect the Adder (the red and the green ones). These signals are wires ( wire ) and must be declared as such.
The syntax for instantiating a module is as follows:
NameModuleInstantiatedNameName (
.nume_intrare_sau_iesire_0 (nume_semnal_legat_la_intrare_sau_iesire_0)
.nume_intrare_sau_iesire_1 (nume_semnal_legat_la_intrare_sau_iesire_1)
//...
.nume_intrare_sau_iesire_n (nume_semnal_legat_la_intrare_sau_iesire_n)
);
So let's see what the Verilog code for the Adder4 module looks like:
module Adder4 (
output [4: 0] out,
input [2: 0] in0,
input [2: 0] in1,
input [2: 0] in2,
input [2: 0] in3
);
//define the connecting wires
wire [3: 0] subsum0;
wire [3: 0] subsum1;
//instantiating the modules
Adder adder0 (
.out (subsum0), //the called out of the adder0 instance links to the submodule thread
.in0 (in0), //at the input called in0 of the adder0 instance, the input in0 of the module
.in1 (in1) //at the input called in1 of the adder0 instance connects the input in1 of the module
);
Adder adder1 (
.out (subsum1), //the outgoing output of the adder1 instance binds to the subsume1
.in0 (in2), //at the input called in0 of the adder1 instance, the in2 input of the module
.in1 (in3) //at the input called in1 of the adder1 instance it binds the input in3 of the module
);
Adder adder2 (
.out (out), //the outgoing output of the adder2 instance links to the outgoing module
.in0 (subsum0), //at the input called in0 of the adder2 instance, the thread subsum0
.in1 (subsum1) //at the input called in1 of the adder2 instance, the thread subsum1
);
endmodule
Note: Adder0 and adder1 have links to 3-bit and 4-binary inputs, although their ports have 4 or 5 bits (inputs and outputs). In this case, the bindings are aligned to the least significant bit, and a mismatch port is generated. Although the programs we use support the above code, there are programs that do not support such constructions, and stop eroding. To be very rigorous, we will use the concatenation operator to correct the code in the following way (more about the operators you will find below):
module Adder4 (
output [4: 0] out,
input [2: 0] in0,
input [2: 0] in1,
input [2: 0] in2,
input [2: 0] in3,
);
//define the binding yarns
wire [4: 0] subsum0; //define the 5-bit threads because the output of adder0 and adder1 is 5 bits
wire [4: 0] subsum1;
//instantiating the modules
Adder adder0 (
.out (subsum0), //the called out of the adder0 instance links to the submodule thread
.in0 ({1'b0, in0}), //at the input called in0 of the adder0 instance binds a bit 0 concatenated with the input in0 of the module
.in1 ({1'b0, in1}) //at the input called in1 of the adder0 instance binds a 0 bit concatenated with the in1 input of the module
);
Adder adder1 (
.out (subsum1), //the outgoing output of the adder1 instance binds to the subsume1
.in0 ({1'b0, in2}), //at the input called in0 of the adder1 instance binds a bit 0 concatenated with the input in2 of the module
.in1 ({1'b0, in3}) //at the input called in1 of the adder1 instance, a bit 0 concatenated with the input of the module
);
Adder adder2 (
.out (out), //the outgoing output of the adder2 instance links to the outgoing module
.in0 (subsum0 [3: 0]), //at the input called in0 of the adder2 instance, the least significant 4 bits of the submodule thread
.in1 (subsum1 [3: 0]) //At the input called in1 of the adder2 instance, the least significant 4 bits of the submode thread 1
);
endmodule
Test modules (not synonymous)
The test modules are used to check the functionality of another synthesizable module. The figure below shows the block diagram for a 4-bit checker module. A generic test module follows a few clear rules:
- for each input of the test module, a variable ''' of the same size as the input is used to generate circuit stimuli;
- for each output of the test module, a wire type variable of the same size as the output used for behavioral verification (usually by waveform display) is defined;
- instantiates the test module and links the previously defined variables to the inputs and outputs of the instance;
- Write a stimulus generator (an ''block) in which a timed sequence of input transitions is programmed;
- Use simulation software to run the test and see the waveforms.
Thus, the test module for the 4-bit adder will look like this:
module AdderTester;
//this is the definition of variables and wires
//for driving signals
reg [3: 0] i0;
reg [3: 0] i1;
wire [4: 0];
//this is where the stimulus is added for the module
initial begin
i0=0;
i1=0;
#5 i0=3;
#2 i0=2;
i1=1;
#3 i0=1;
i1=5;
#5 $ stop ();
end
//this is where the tested module is instantiated
Adder deviceUnderTest (
.out (a)
.in0 (I0),
.in1 (i1)
)
endmodule
The initial block is used to give input values to the test module. He starts execution at time t=0. Each line is executed at the same time point until the #operator who encounters time passes is encountered. Thus, in the example above, the first two lines are executed at t=0, line 3 is executed at t=5, lines 4 and 5 at t=7, lines 6 and 7 at t=10 and the last line at t=15. The call to $ stop () determines the end of the simulation.
Clock signal in test modules
The keyword forever is used to execute a assignment or function call repeatedly until the end of the simulation. This is particularly useful for generating a clock signal. The next sequence of code generates a clock signal with two time units:
reg clock;
initial begin
clock=0;
forever #1 clock = ~clock;
end
Verilog syntax
Constants
Constants are numerical values. For each value, specify the number of bits that it represents and the base in which it is written. For example, 8'b111 is an 8-bit constant whose value in binary is 111 (ie in decimal, 7). In the same way, 16'd10 represents 10 in decimal represented by 16 bits. It is possible to specify the value without the number of bits or base (in which case the default is the decimal one, and the number of bits is approximated by the compiler).
Operators
Arithmetic Operators
| Operation | Operator | Example |
| Addition | + | a + b |
| Substraction | - | a - b |
| Multiplication | * | a * b |
| Division | / | a /b |
Logical Operators
| Operation | Operator | Example |
| Equality | == | a == b |
| Non-equality | != | a!=b |
| Less | < | a <b |
| Less or equal | <= | a <= b |
| More | > | a> b |
| More or equal | >= | a>=b |
Bitwise logic operators
| Operation | Operator | Example |
| And | & | a & b |
| Or | | | and | b |
| Exclusive or | ^ | a ^ b |
Bitwise logical operators
| Operation | Operator | Example |
| Negation | ~ | ~ b |
| And the bits of a signal | & | & a |
| Or the bits of a signal | | | | a |
| Or exclusively on the bits of a signal | ^ | ^ a |
Bit shift operators
| Operation | Operator | Example |
| Left Shift | << | a << b |
| Right Shift | >> | a >> b |
Bit access operator
Given a n-bit signal, the access operator to a signal bit sub-sequence is [m: k] where m and k are indexes of the desired bits with n < m < k. For example:
reg [31: 0] a_register;
wire [7: 0] a_wire;
wire another_wire;
assign a_wire = a_register [30:23]; //the wire "a_wire" takes the value of the bit sequence from 23 to 30 in the register "a_register"
assign another_wire = a_wire [3]; //the "another_wire" wire will take the bit 3 value of the "a_wire" signal that is the bit 26 of the "a_register"
Concatenation operator
The concatenation operator is '{' and '}'. Thus, a series of semicolon-separated and closed signals between two braces will result in a single signal of size equal to the sum of the dimensions of the component signals.
wire [3: 0] and;
wire [4: 0] b;
wire c;
wire [9: 0] d;
//the signal d is formed by the concatenation of the signals a, b, c
//where a is in the most significant position and c
//in the least significant position
assign d={a, b, c};
Replication operator
The replication operator is used when it is desired to replicate a large or unknown number of times (given as a parameter). Thus, the construction {n {m}} represents the signal m multiplied by n times.
wire a;
wire [4: 0] b;
wire [7: 0] c;
wire [15: 0] d;
assign b={5 {a}}; //b will take the value of a, replicated 5 times
assign d={2 {c}}; //d will take the value of c (8 bits) replicated 2 times
Blocks and conditional operators
The conditions can be expressed in three ways:
- using the known conditional operator in C (condition ?_value_value: value_for_fals);
- using the if - else construction;
- using the case-endcase case or endcase case or endcase case.
The conditional operator can be used in any type of block. Example:
wire a;
wire [3: 0] b;
wire [3: 0] c;
wire [3: 0] d;
assign b=a? c: d; //if it is true (ie if it is equal to 1), then b takes the value of c, otherwise, b is the value of d
Blocks' if - else , case - endcase can only be used in blocks always. Example:
wire a;
reg [3: 0] b;
wire [3: 0] c;
wire [3: 0] d;
always @ (a or c or d) begin
if (a) begin
b=c;
end else begin
b=d;
end
end
Example case - endcase:
wire [1: 0] and;
reg [3: 0] e;
wire [3: 0] c;
wire [3: 0] d;
//if a is equal to 0, then it takes the value of c
//if a is equal to 1, then it takes the value of d
//in any other case, b is 0
always @ (a or c or d) begin
case (a)
2'b00: e=c;
2'b01: e=d;
default: e=3'b000;
endcase
end